Ctrl+K

Covariance models

Covariance models#

Download#

Graphical LASSO#

  • A different model for covariances: models \(\Theta=\Sigma^{-1}\).

  • Problem is

\[ \text{minimize}_{\Theta: \Theta=\Theta', \Theta \geq 0} - \frac{n}{2} \log |\Theta| + \frac{1}{2}\text{Tr}(XP_c^TX\Theta) + \lambda \|\Theta\|_1^- \]

where \(\|\cdot\|^-_1\) does not penalize diagonal part of \(\Theta\).

  • As we have a likelihood we can in principle use cross-validation to choose \(\lambda\).

What’s the point?#

Graphical models#

  • Graphical models (can) encode conditional independences.

  • In Gaussian models these are represented by 0 in \(\Sigma^{-1}\)

Example#

Multivariate normal#

  • Figure (a) represents \(X \perp Z | Y\)

  • Implies that \(\Sigma_{XZ}=0\).

  • Formally if \(W \sim N(0, \Theta^{-1})\) and \(\Theta_{ij}=0\) then \(W_i \perp W_j | W_{-\{i,j\}}\).

Relation to log-linear models#

  • Suppose \(X, Y, Z\) were discrete variables and \(N\) is a contingency table with axes X, Y, Z.

  • The above conditional independence can be encoded as

glm(N ~ X + Y + Z + X:Y + Y:Z, family=poisson)

  • Limiting interactions to 2nd order, any undirected graph can be converted to such a model.

  • Figure (d) is the model

glm(N ~ X + Y + Z + W + X:Y + Y:Z + Z:W, family=poisson)

Back to graphical LASSO#

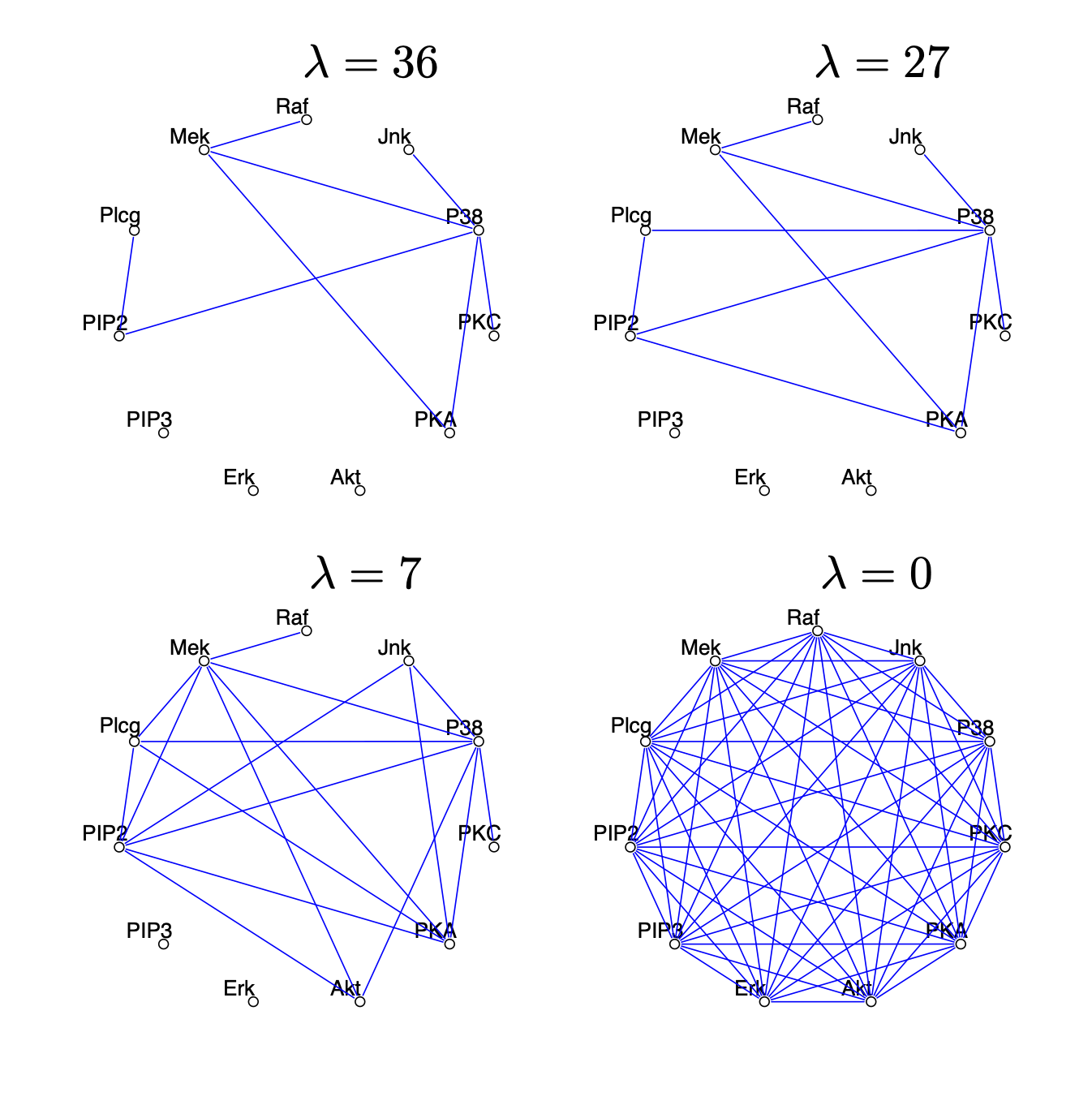
  • Choosing \(\lambda\) sets the sparsity level.

  • The graphical LASSO tries to make decisions about all \(\binom{p}{2}\) conditional independencies simultaneously.

Fitting graphical LASSO#

  • If \(p\) grows, then directly using the likelihood becomes expensive (gradients is \(O(p^3)\) for inverting \(p \times p\))…

  • Graphical LASSO algorithm solves by iterative LASSO solves…

Graphical LASSO#

#| echo: true
library(glasso)
flow = read.table('http://www.stanford.edu/class/stats305c/data/sachs.data', sep=' ', header=FALSE)
G = glasso(var(flow)/1000, 27)

library(corrplot)
Theta = G$wi
Theta = Theta / outer(sqrt(diag(Theta)), sqrt(diag(Theta)))
corrplot(Theta, method='square')

corrplot 0.95 loaded
../_images/265547e1a9869c4e538bf6fefffcf3e6eec7a16c9f3482bcd53148116a1f334e.png

Using sklearn#

CV curve#

Best estimator#

Alternative approaches#

\[ X_j | X_{-j} \sim N(\theta_j, \Sigma_j) \]

  • Further,

\[ \theta_j[k] = -\frac{\Theta_{jk}}{\Theta_{jj}} \]

  • Therefore, \(\theta_j[k] = 0 \iff \Theta_{jk}=0\) \(\implies\) conditional independencies of interest can be learned by regressions

lm(X[,j] ~ X[,-j])

  • Can induce sparsity by

glmnet(X[,-j], X[,j])

Combining edge sets#

  • One downside to this approach is that we make two decisions about \(X_j \perp X_k | X_{-\{j,k\}}\):

    • Once when response is \(X[,j]\), the other when the response is \(X[,k]\).

Solutions#

  • Make a decision using AND or OR…

Or#

  • Maybe, we could we tie the parameters together in the \(p\) different LASSO problems?

  • This is essentially pseudo-likelihood (more shortly)

Combining factor analysis and low-rank#

  • We finished Factor Analysis section off with a convex relaxation of factor analysis / low-rank

  • Can combine this with graphical LASSO

\[ \text{minimize}_{(\Phi, \Omega): \Phi-\Omega \geq 0, \Omega \geq 0} = - \frac{n}{2} \log |\Phi - \Omega| + \text{Tr}(X^TR_cX(\Phi - \Omega)) + \lambda_1 \|\Omega\|_* + \lambda_2 \|\Phi\|_1^-\]

Extension to mixed data#

  • What if \(X \in \mathbb{R}^p\) is continuous but \(Y \in \{1,2,3,...,L\}\) discrete?

  • What is the analog of

glm(N ~ X + Y + X:Y, family=poisson)

2nd-order potentials (first order interactions in log-linear models)#

\[ p(x, y; \Theta) \propto \exp \left[ -\frac{1}{2} \sum_{s=1}^p \sum_{t=1}^p \beta_{st} x_s x_t + \sum_{s=1}^p \alpha_s x_s + \sum_{s=1}^p \sum_{l=1}^L \rho_{sl} \cdot y_l \cdot x_s + \sum_{l=1}^L \theta_l \cdot y_l \right] \]

  • Can have multiple discrete variables as well (with a single variable the above model is LDA - linear discriminant analysis)

\[ p(x, y; \Theta) \propto \exp \left[ -\frac{1}{2} \sum_{s=1}^p \sum_{t=1}^p \beta_{st} x_s x_t + \sum_{s=1}^p \alpha_s x_s + \sum_{s=1}^p \sum_{j=1}^q \rho_{sj} (y_j) x_s + \sum_{j=1}^q \sum_{r=1}^q \phi_{rj} (y_r, y_j) \right] \]

Mixed graphical models#

Fitting mixed models#

  • For glasso there is an explicit likelihood to maximize, but mixed models will have some awful intractable normalizing constant…

  • BUT for each variable, our modeling choices have nice conditional likelihoods.

    • For continuous variables \(X_i\) is Gaussian with mean and covariance determined by \(\Theta\).

    • Discrete variables \(Y_j\) are multinomial with specific multinomial logistic models determined by \(\Theta\)

(Penalized) pseudo-likelihood#

\[ \sum_{s=1}^p \log f_{\Theta}(X_s|X_{-s}, Y) + \sum_{j=1}^q \log f_{\Theta}(Y_j|Y_{-j}, X) + {\cal P}(\Theta) \]

  • Often, \({\cal P}\) will separate over variables but the individual likelihoods tie parts of \(\Theta\) together…

Pseudo-likelihood#

  • Consider a simple Ising model: i.e. a binary random vector \(B \in \{0,1\}^J\) with mass function

\[ f_{c_1,c_2}(b_1,\dots, b_k) \propto \exp\left( b_j\left(c_1 + c_2 \sum_{(j,k):j \neq k} A_{jk} b_j b_k \right)\right) \]

  • Matrix \(A\) an adjacency matrix for some graph.

  • The normalizing constant requires summing over \(2^J\) states…

Conditional likelihoods#

  • For any \(j\),

\[ f_{\theta}(b_j | b_{-j}) \propto \exp\left(b_j \left(c_1 + c_2 \sum_{k: k \neq j} b_k\right)\right) \]

  • This conditional has a simple normalizing constant

\[ 1 + \exp\left(c_1 + c_2 \sum_{k: k \neq j} b_k\right) \]

  • Summing log over \(j=1, \dots, J\) yields an expression that’s simple to optimize

\[ \sum_{j=1}^J \left(c_1 \cdot b_j + c_2 \sum_{(j, k):k \neq j} b_j b_k\right) - \sum_{j=1}^J \log\left(1 + \exp\left(c_1 + c_2 \sum_{k: k \neq j} b_k\right)\right) \]

  • Working in this model, at “true” parameters \((c_1^*, c_2^*)\) we have the gradient of the pseudo-likelihood is centered (just like the likelihood).

Yet another model for covariance: additive#

  • We’ve considered two general models for covariance so far:

    • Diagonal + Low-Rank (PPCA & Factor Analysis)

    • Sparse precision (Graphical LASSO)

    • Combination of the two…

Additive model#

  • Given \(C_j \succeq 0, 1 \leq j \leq k\)

\[ \Sigma = \sum_{j=1}^k \alpha_j C_j, \qquad \alpha_j > 0 \]

Generative model#

\[\begin{split} \begin{aligned} Z_j &\sim N(0, \alpha_j C_j), \qquad (\text{independently}) \\ X &= \sum_{j=1}^k Z_j \end{aligned} \end{split}\]

EM for additive model#

Complete (negative) log-likelihood#

\[ \sum_{i=1}^n \left(\sum_{j=1}^k \frac{n}{2}\log \det(\alpha_j C_j) + \frac{1}{2\alpha_j} \text{Tr}(C_j^{-1}Z_{ij}Z_{ij}') \right) \]

E-step#

  • Given current \(\alpha_{\text{cur}}=\alpha_c\) we need to compute

\[ \mathbb{E}_{\alpha_c}[Z_{ij}Z_{ij}'|X_i] \]

\(M\)-step#

\[ \alpha_{j,\text{new}} = \frac{1}{n} \sum_{i=1}^n \text{Tr}\left(C_j^{-1}\mathbb{E}_{\alpha_c}[Z_{ij}Z_{ij}'|X_i]\right) \]

A generalization#

  • Given \(D_j, 1 \leq j \leq k\)

\[ \Sigma = \sum_{j=1}^k D_j \bar{\Sigma}_j D_j', \qquad \bar{\Sigma}_j \succeq 0 \]

  • Could impose structure on \(\bar{\Sigma}_j\) (e.g. diagonal, \(c \cdot I\), etc)

  • This is (stylized) version of RFX covariance

Generative model#

\[\begin{split} \begin{aligned} Z_j &\sim N(0, \bar{\Sigma}_j), \qquad (\text{independently}) \\ X &= \sum_{j=1}^k D_j Z_j \end{aligned} \end{split}\]

EM for RFX model#

Complete (negative) log-likelihood (\(n=1\))#

\[ \sum_{j=1}^k \frac{1}{2}\log \det(\bar{\Sigma}_j) + \frac{1}{2} \text{Tr}(\bar{\Sigma}_j^{-1}Z_{j}Z_{j}') \]

E-step#

  • Given current estimates \(\bar{\Sigma}_c=(\bar{\Sigma}_{j,c}, 1 \leq j \leq k)\), we need to compute

\[ \mathbb{E}_{\bar{\Sigma}_c} [Z_jZ_j'|X] \]

M-step#

  • Unrestricted MLE having observed \(\mathbb{E}_{\bar{\Sigma}_c} [Z_jZ_j'|X]\)…

More realistic RFX setup#

Generative model#

  • Switching to errors notation \(\epsilon\)…

\[\begin{split} \begin{aligned} Z_{ij} &\sim N(0, \bar{\Sigma}_j), \qquad (\text{independently}) \\ \epsilon_i &= \sum_{j=1}^k D_{ij} Z_{ij} \end{aligned} \end{split}\]

  • Some of the \(Z_{ij}\)’s will be of different sizes (depending on how many observations subject \(i\) contributes…)

Complete (negative) log-likelihood#

\[ \sum_{i=1}^n \sum_{j=1}^k \frac{n}{2}\log \det(\bar{\Sigma}_j) + \frac{1}{2} \text{Tr}(\bar{\Sigma}_j^{-1}Z_{ij}Z_{ij}') \]

  • Need to compute

\[ \mathbb{E}_{\bar{\Sigma}_c} [Z_{ij}Z_{ij}'|\epsilon_i] \]

An example in a little more detail#

Repeated measures#

  • For subject \(i\) with \(n_i\) measurements $\( \begin{aligned} \alpha_i &\sim N(0, \sigma^2_R) \\ \epsilon_{i} & \sim N(0, \sigma^2_M \cdot I) \\ X_{i} &= \alpha_i 1_{n_i} + \epsilon_{i} \end{aligned} \)$

  • \(\implies\) contribution of subject \(i\) to complete (negative) log-likelihood is

\[ \frac{1}{2} \log(\sigma^2_{R}) + \frac{1}{2 \sigma^2_R} \alpha_i^2 + \frac{n_i}{2} \log(\sigma^2_M) + \frac{1}{2 \sigma^2_{M}} \text{Tr}(\epsilon_i \epsilon_i') \]

  • Total covariance is \(\sigma^2_R C_R + \sigma^2_M \cdot I\) with \(C_R\) block diagonal

M-step \(\sigma^2_R\)#

  • Given \(\theta_c = (\sigma^2_{M,c}, \sigma^2_{R,c})\):

\[\begin{split} \begin{aligned} \alpha_i | X_i & \sim N\left(\sigma^2_{R,c}1_{n_i}'\left( \sigma^2_{R,c} 1_{n_i}1_{n_i}' + \sigma^2_{M,c} I\right)^{-1}X_i, (\sigma^2_{R,c})^2 1_{n_i}'\left( \sigma^2_{R,c} 1_{n_i}1_{n_i}' + \sigma^2_{M,c} I\right)^{-1}1_{n_i}\right) \\ \mathbb{E}_{\theta_c}[\alpha_i^2|X_i] &= (\sigma^2_{R,c})^4\biggl[X_i' \left(\sigma^2_{R,c} 1_{n_i}1_{n_i}' + \sigma^2_{M,c} I\right)^{-1} 1_{n_i}1_{n_i}'\left( \sigma^2_{R,c} 1_{n_i}1_{n_i}' + \sigma^2_{M,c} I\right)^{-1} X_i + \\ & \qquad 1_{n_i}'\left( \sigma^2_{R,c} 1_{n_i}1_{n_i}' + \sigma^2_{M,c} I\right)1_{n_i} \biggr] \end{aligned} \end{split}\]

  • Sherman-Morrison-Woodbury simplifies above expression, leads to closed-form update \(\sigma^2_{R,u}\)

  • ECM performs blockwise updates to parameters… does not fully maximize before subsequent E-step

M-step \(\sigma^2_M\)#

  • Given partially updated \(\theta_{c+1/2} = (\sigma^2_{M,c}, \sigma^2_{R,u})\):

\[\begin{split} \begin{aligned} \epsilon_i | X_i & \sim N\left(\sigma^2_{M,c}\left( \sigma^2_{R,u} 1_{n_i}1_{n_i}' + \sigma^2_{M,c} I\right)^{-1}X_i, (\sigma^2_{M,c})^2 \left( \sigma^2_{R,u} 1_{n_i}1_{n_i}' + \sigma^2_{M,c} I\right)^{-1}\right) \\ \mathbb{E}_{\theta_c}[\epsilon_i \epsilon_i'|X_i] &= (\sigma^2_{M,c})^4\biggr[X_i \left(\sigma^2_{R,u} 1_{n_i}1_{n_i}' + \sigma^2_{M,c} I\right)^{-2} X_i' + \\ & \qquad \left( \sigma^2_{R,u} 1_{n_i}1_{n_i}' + \sigma^2_{M,c} I\right) \biggr] \end{aligned} \end{split}\]

  • This is ECM, Meng and Rubin (1993).

  • Usefulness of the approach a little more obvious in the presence of mean parameters:

    • Fix \((\sigma^2_M, \sigma^2_R)\) and estimate \(\beta\),

    • Fix \(\beta\) and estimate \((\sigma^2_M, \sigma^2_R)\).

ECME#

  • For any block of \(\theta\), can use the (conditional / blockwise) MLE

  • For update of \(\sigma^2_M\), fixing \(\sigma^2_R=\sigma^2_{R,u}\) compute

\[ \text{argmax}_{\sigma^2_M} \sum_{i=1}^n -\frac{1}{2} \log \det(1_{n_i} 1_{n_i'} + \sigma^2_R I_{n_i}) - \frac{1}{2}\left(X_i'\left(\sigma^2_{R,u} 1_{n_i} 1_{n_i'} + \sigma^2_R I_{n_i}\right)^{-1}X_i\right) \]

  • Both ECM and ECME share EM’s ascent property…

Wrapping up#

  • We’ve discussed several models of covariance…

  • While not difficult to describe, only some are relatively easy to use in R:

    • prcomp

    • doppca

    • factanal

    • glasso

    • lme4 (for RFX, not discussed here)

  • Would be nice to have all of these methods easily available in code…

  • PCA gets used a lot, at least partly because it’s implementation is so simple…

  • We saw that sklearn has some decent implementations of PCA / FactorAnalysis / Graphical LASSO

  • Would being a Bayesian make life easier?

Contents