Ctrl+K

PCA I

PCA I#

Download#

PCA#

Two views#

  • Low-rank matrix approximation

  • Maximal variance projection

Low-rank approximation#

  • Consider problem

\[ \text{minimize}_{A \in \mathbb{R}^{n \times k},B \in \mathbb{R}^{q \times k}} \|R_cX-AB^T\|^2_F \]

with

\[ R_c = \left(I - \frac{1}{n}11^T\right) \]

  • This is reduced rank regression objective with \(\tilde{Y}=R_cX\), \(\tilde{X}=I\), \(\Sigma=I\).

  • Going forward, we’ll somtimes drop \(R_c\) by assuming that \(R_cX=X\), i.e. that it has already been centered.

Solution#

  • Our reduced-rank regression solution told us to look at \(\tilde{W}\), \(k\) leading eigenvectors of

\[ XX^T \]

  • Then, we take

\[\begin{split} \begin{aligned} \tilde{A} &= \tilde{W} \\ \tilde{B} &= X^T\tilde{A}(\tilde{A}^T\tilde{A})^{-1} \\ &= X^T\tilde{A} \end{aligned} \end{split}\]

Relation to SVD#

  • Given matrix \(M \in \mathbb{R}^{n \times p}\) (assume \(n>p\)) there exists an SVD

\[ M = U_{n \times p} D_{p \times p} V_{p \times p}^T \]

Properties#

\[\begin{split} \begin{aligned} U^TU &= I_{p \times p} \\ D &= \text{diag}(d_1 \geq d_2 \geq \dots \geq d_p \geq 0) \\ V^TV &= \text{I}_{p \times p} \end{aligned} \end{split}\]

  • Consider

\[ MM^T = UD^2U^T \]

  • Eigen-decomposition of \(MM^T\) can be found from SVD of \(M\).

  • Similarly

\[ M^TM = VD^2V^T. \]

  • Finally,

\[ M^TU = VD \]

  • Can absorb \(D\) into \(U\) by writing

\[ M = (UD)V^T \]

Back to reduced rank#

  • Our reduced rank solution with \(X=UDV^T\) picks

\[\begin{split} \begin{aligned} \hat{A} &= U[,1:k] \\ \hat{B} &= D[1:k,1:k] V[,1:k]^T \end{aligned} \end{split}\]

  • More common to think of rank-\(k\) PCA in terms of first \(k\) scores

\[ U[,1:k] D[1:k,1:k] \]

and loadings

\[ V[,1:k] \]

A second motivation#

  • Could also consider the problem

\[ \text{minimize}_{A \in \mathbb{R}^{p \times k}, B \in \mathbb{R}^{p \times k}} \|X - XAB^T\|^2_F \]

  • Also a reduced rank problem whose solutions are projections onto a k-leading eigenspace of \((X^TX)\).

  • This one clearly isn’t a likelihood – \(X\) appears as response and design.

Maximal variance#

  • Minimizing first over \(A\), we see this is equivalent to solving this problem

\[ \text{minimize}_{P_k} \|X - XP_k\|^2_F \]

where \(P_k\) is a projection matrix of rank \(k\).

  • Equivalently, we solve (recall \(R_cX=X\))

\[ \text{minimize}_{P_k} \text{Tr}(X^TR_cX) - \text{Tr}(P_kX^TR_cXP_k) \]

  • This is the same as

\[ \text{maximize}_{P_k} \text{Tr}(P_kX^TR_cXP_k) \]

  • Rank \(k\) PCA captures \(k\) dimensional subspace of features that maximizes variance…

Population version#

  • The maximizing variance picture lends itself to a population version

  • Thinking of rows of \(X\) as IID with law \(F\), let \(\Sigma = \text{Var}_F(X[1,])\)

\[ \text{minimize}_{P_k} \text{Tr}(\Sigma) - \text{Tr}(P_k\Sigma P_k) \iff \text{maximize}_{P_k} \text{Tr}(P_k \Sigma P_k) \]

  • Solution is to choose top \(k\) eigen-subspace of \(\Sigma\)…

PCA = SVD#

  • Given data matrix \(X \in \mathbb{R}^{n \times p}\) with rows \(X[i,] \overset{IID}{\sim} F\), the sample PCA can be described by the SVD of \(R_cX\)

  • As \(V\) can be thought as an estimate of \(\Gamma\) in an SVD of

\[ \text{Var}_F(X) \approx \Gamma \Lambda \Gamma^T \]

we might write \(V = \widehat{\Gamma}\).

  • Columns of \(\widehat{\Gamma}\) are the loadings of the principal components while columns of \(UD = \hat{Z}\) are the (sample) principal components scores.

Scaling#

  • Common to scale columns of \(X\) to have standard deviation 1.

  • In this case, we are really computing the PCA of

\[ R_c X \text{diag}(S)^{-1} \]

  • Scalings are

\[ S^2_{i,i} = \frac{1}{n-1}X[,i]^TR_cX[,i] = {\tt sd(X[,i])}^2 \]

Synthetic example#

#| echo: true
n = 50
p = 10
X = matrix(rnorm(n*p), n, p)
R_c = diag(rep(1, n)) - matrix(1, n, n) / n
SVD_X = svd(R_c %*% X)
Z = SVD_X$u %*% diag(SVD_X$d)
Gamma_hat = SVD_X$v
pca_X = prcomp(X, center=TRUE, scale.=FALSE)
names(pca_X)
  1. 'sdev'
  2. 'rotation'
  3. 'center'
  4. 'scale'
  5. 'x'

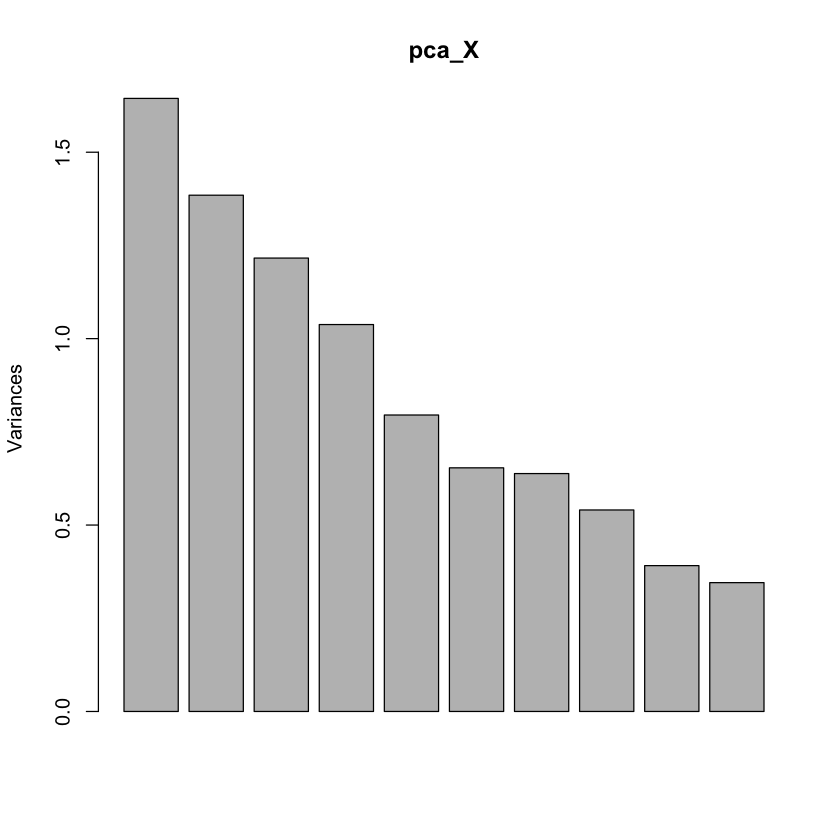
Screeplot: is there an elbow?#

plot(pca_X) # Screeplot
c(varZ2=var(Z[,2]))
varZ2: 1.38470878741862
../_images/e00a77d5d3e4e52933ed6d35a55d42a37b1d4b116fadb16df3034347bbe3f29b.png

Check loadings#

summary(lm(Gamma_hat[,1] ~ pca_X$rotation[,1]))

Warning message in summary.lm(lm(Gamma_hat[, 1] ~ pca_X$rotation[, 1])):
“essentially perfect fit: summary may be unreliable”

Call:
lm(formula = Gamma_hat[, 1] ~ pca_X$rotation[, 1])

Residuals:
       Min         1Q     Median         3Q        Max 
-4.787e-16 -1.601e-16  6.330e-18  1.643e-16  5.433e-16 

Coefficients:
                     Estimate Std. Error   t value Pr(>|t|)    
(Intercept)         3.294e-17  1.049e-16 3.140e-01    0.762    
pca_X$rotation[, 1] 1.000e+00  3.317e-16 3.015e+15   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.258e-16 on 8 degrees of freedom
Multiple R-squared:      1,	Adjusted R-squared:      1 
F-statistic: 9.089e+30 on 1 and 8 DF,  p-value: < 2.2e-16

Check scores#

plot(Z[,1], pca_X$x[,1], pch=23, bg='red')
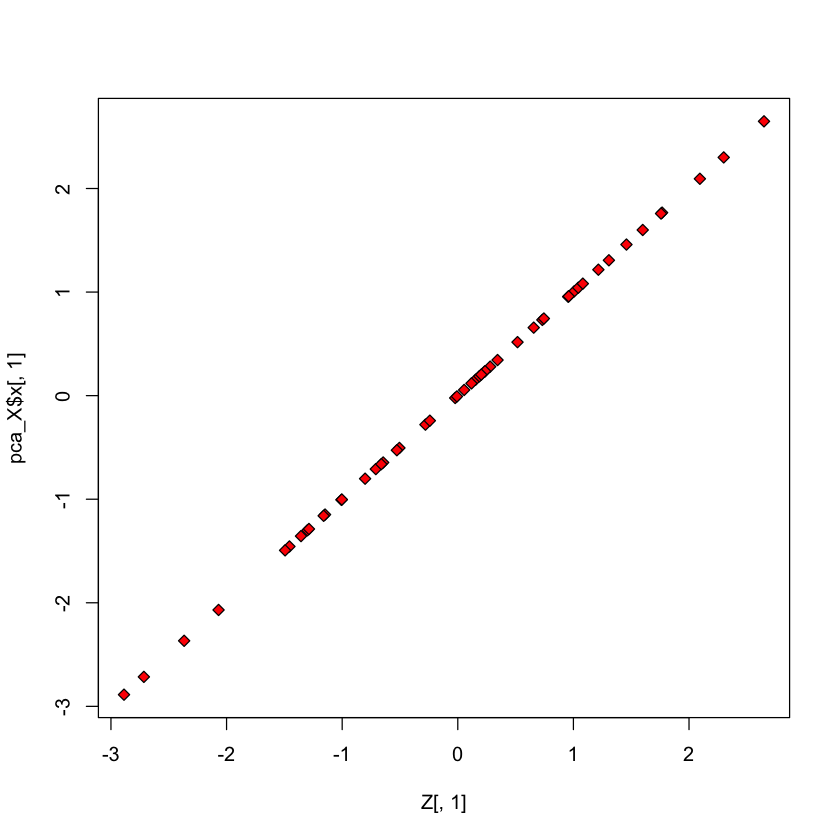
../_images/487c73d8559ceb880c810b8b0caaf9377881a80e1fedf5f4755ae2b018bb7ab8.png

With scaling#

#| echo: true
S_inv = 1/ (sqrt(diag(t(X) %*% R_c %*% X) / 49))
SVD_Xs = svd(R_c %*% X %*% diag(S_inv))
Z_s = SVD_Xs$u %*% diag(SVD_Xs$d)
Gamma_hat_s = SVD_Xs$v
pca_Xs = prcomp(X, center=TRUE, scale.=TRUE)

Check loadings#

#| echo: true
summary(lm(Gamma_hat_s[,1] ~ pca_Xs$rotation[,1]))

Call:
lm(formula = Gamma_hat_s[, 1] ~ pca_Xs$rotation[, 1])

Residuals:
       Min         1Q     Median         3Q        Max 
-4.321e-16 -2.714e-16 -2.976e-17  2.422e-16  5.693e-16 

Coefficients:
                      Estimate Std. Error   t value Pr(>|t|)    
(Intercept)          1.347e-16  1.150e-16 1.171e+00    0.275    
pca_Xs$rotation[, 1] 1.000e+00  3.638e-16 2.749e+15   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.464e-16 on 8 degrees of freedom
Multiple R-squared:      1,	Adjusted R-squared:      1 
F-statistic: 7.555e+30 on 1 and 8 DF,  p-value: < 2.2e-16

Check scores#

plot(Z_s[,1], pca_Xs$x[,1], pch=23, bg='red')
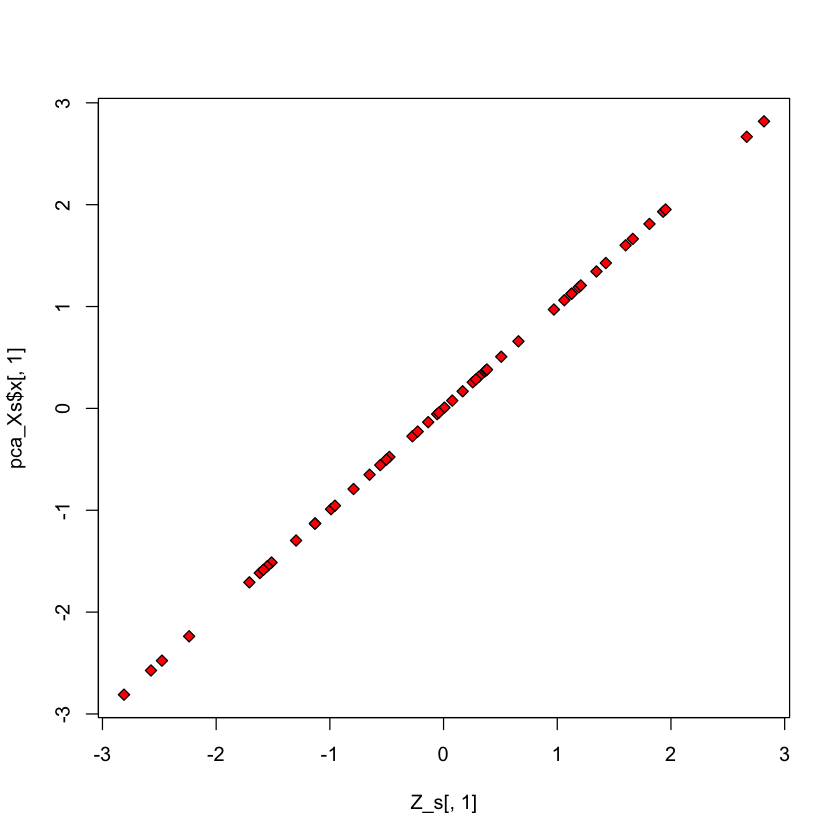
../_images/2759cb8887c460ddf37e85f70b6232e4b5d280d53bee9b854e35570e5b460964.png

Some example applications#

USArrests data#

#| echo: true
pr.out = prcomp(USArrests, scale = TRUE)
names(pr.out)
  1. 'sdev'
  2. 'rotation'
  3. 'center'
  4. 'scale'
  5. 'x'

Output of prcomp#

The center and scale components correspond to the means and standard deviations of the variables that were used for scaling prior to computing SVD

#| echo: true
pr.out$center
pr.out$scale
Murder
7.788
Assault
170.76
UrbanPop
65.54
Rape
21.232
Murder
4.35550976420929
Assault
83.3376608400171
UrbanPop
14.4747634008368
Rape
9.36638453105965

Rotation / loading#

#| echo: true
pr.out$rotation
A matrix: 4 × 4 of type dbl
PC1PC2PC3PC4
Murder-0.5358995-0.4181809 0.3412327 0.64922780
Assault-0.5831836-0.1879856 0.2681484-0.74340748
UrbanPop-0.2781909 0.8728062 0.3780158 0.13387773
Rape-0.5434321 0.1673186-0.8177779 0.08902432

Biplot#

#| echo: true

biplot(pr.out)
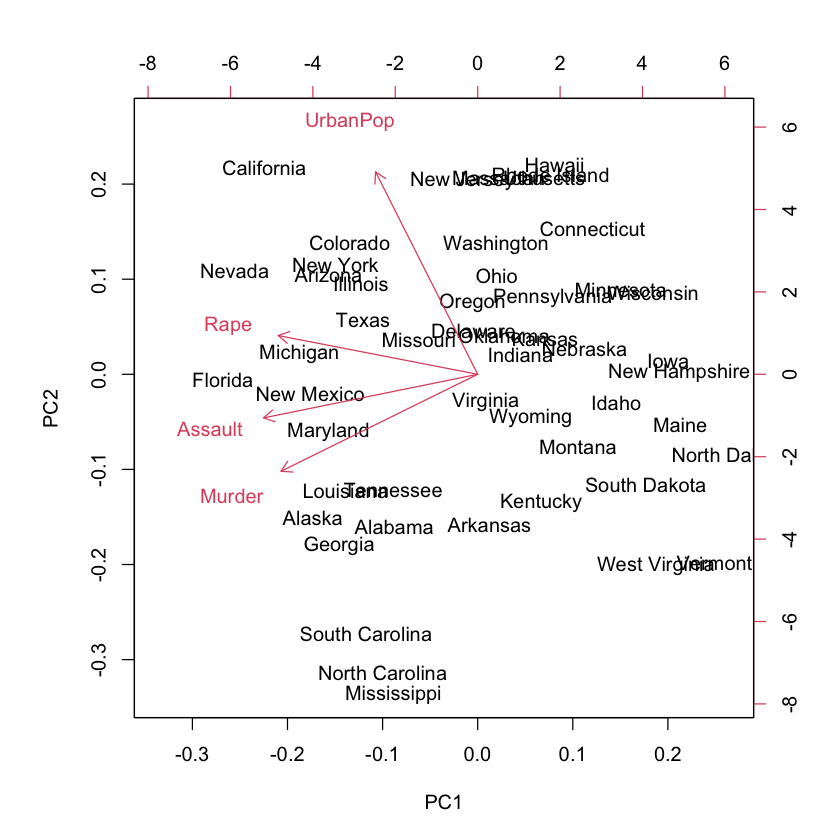
../_images/0ff3c705c234d875ecb9b0bc43afce6467adf24b6b57ed2d5789e1b6b9bcc2c4.png

Variance explained#

#| echo: true
pr.out$sdev
pr.var = pr.out$sdev^2
pr.var
  1. 1.57487827439123
  2. 0.994869414817765
  3. 0.597129115502526
  4. 0.41644938195396
  1. 2.48024157914949
  2. 0.989765152539841
  3. 0.35656318058083
  4. 0.173430087729835
par(mfrow = c(1, 2))
pve = pr.var / sum(pr.var)
plot(pve, xlab = "Principal Component",
    ylab = "Proportion of Variance Explained", ylim = c(0, 1),
    type = "b")
plot(cumsum(pve), xlab = "Principal Component",
    ylab = "Cumulative Proportion of Variance Explained",
    ylim = c(0, 1), type = "b")
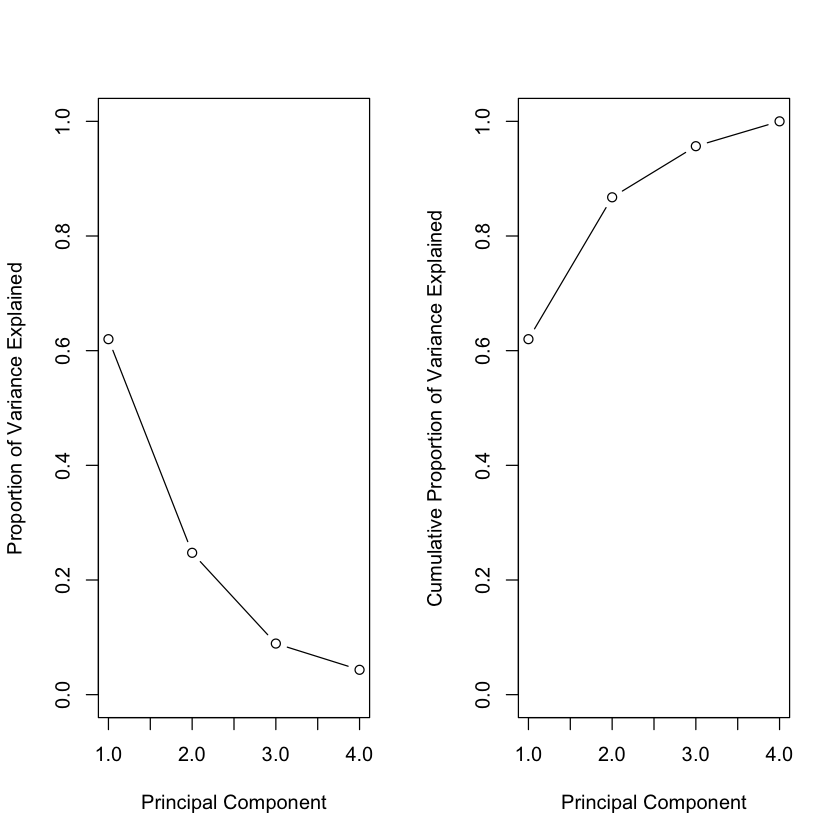
../_images/94536feba6cb2bb568714b1dcadbb15310c21ad8f207fc1e6843dc769afc2203.png

Congressional voting records (1984) – UCI#

#| echo: true
voting_data = read.csv('https://archive.ics.uci.edu/ml/machine-learning-databases/voting-records/house-votes-84.data', header=FALSE)
head(voting_data)
voting_X = c()
for (i in 2:7) {
    voting_data[,i] = factor(voting_data[,i], c('n', '?', 'y'), ordered=TRUE)
    voting_X = cbind(voting_X, as.numeric(voting_data[,i]))
}
pca_votes = prcomp(voting_X, scale.=TRUE)
dem = voting_data[,1] == 'democrat'
repub = !dem
A data.frame: 6 × 17
V1V2V3V4V5V6V7V8V9V10V11V12V13V14V15V16V17
<chr><chr><chr><chr><chr><chr><chr><chr><chr><chr><chr><chr><chr><chr><chr><chr><chr>
1republicannynyyynnny?yyyny
2republicannynyyynnnnnyyyn?
3democrat ?yy?yynnnnynyynn
4democrat nyyn?ynnnnynynny
5democrat yyynyynnnny?yyyy
6democrat nyynyynnnnnnyyyy
 
#| echo: true
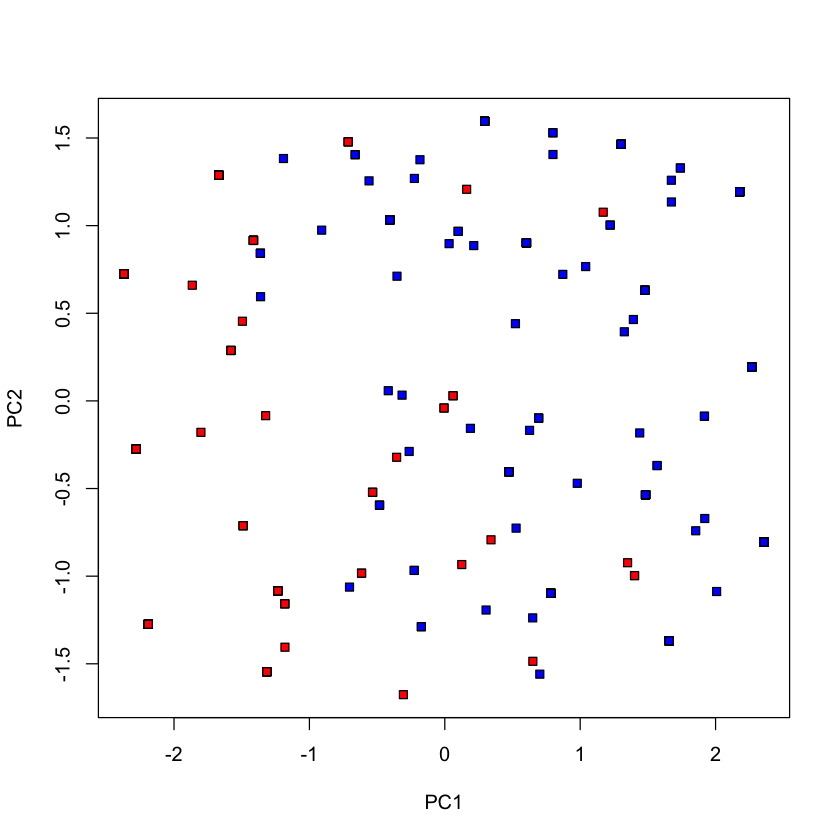
plot(pca_votes$x[,1], pca_votes$x[,2], type='n', xlab='PC1', ylab='PC2')
points(pca_votes$x[dem, 1], pca_votes$x[dem, 2], pch=22, bg='blue')
points(pca_votes$x[repub, 1], pca_votes$x[repub, 2], pch=22, bg='red')
dim(voting_data)
  1. 435
  2. 17
../_images/863dd68ccee21bf3a129ee193b35ecf049c5f5e75dc0d7aa4888a68e2411cc17.png 
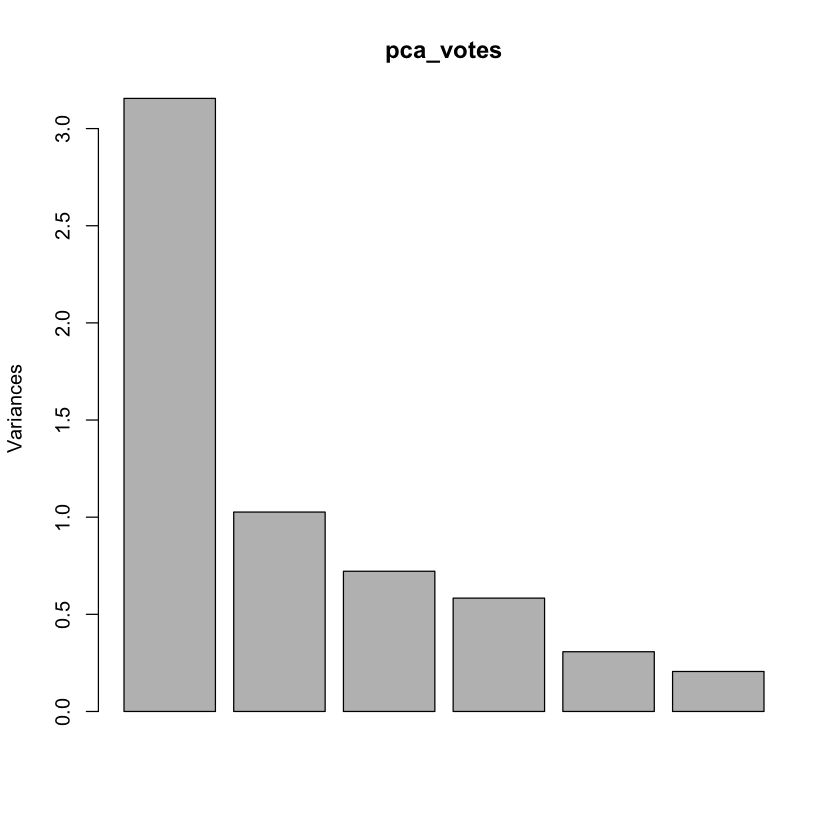
plot(pca_votes)
../_images/86e71e1e8900a733ce8c3bc6f94dee677664bc521c7022e52468ea0dcad8c8e3.png

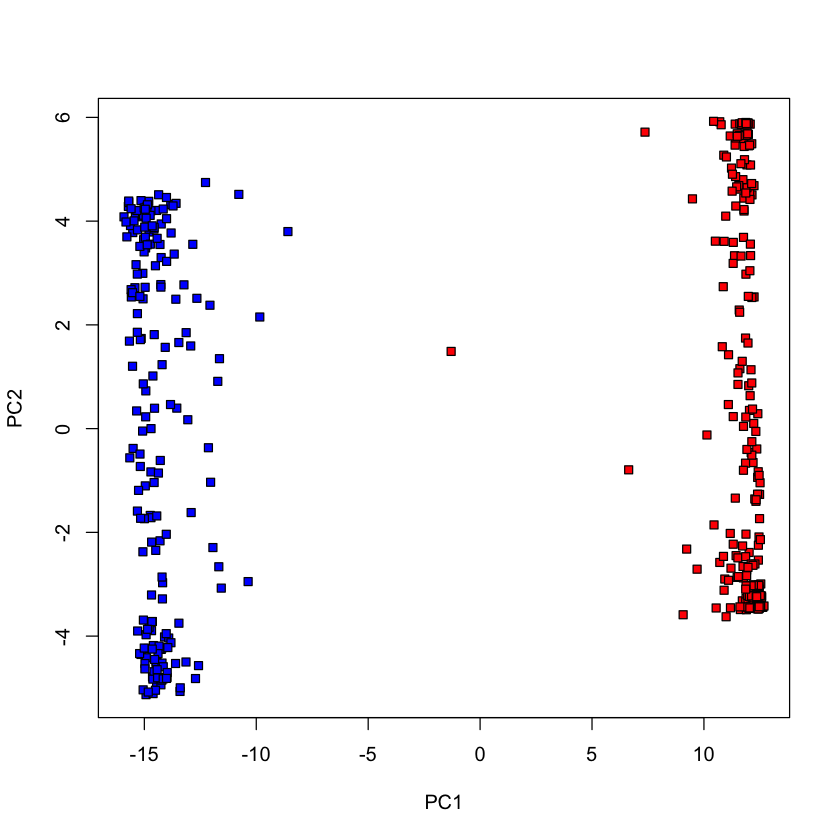
Congress of 2017#

voting_2017 = read.csv('http://stats305c.stanford.edu/data/votes2017.csv', header=TRUE)
dim(voting_2017)
dem_2017 = voting_2017$party == 'D'
repub_2017 = !dem_2017
pca_votes_2017 = prcomp(voting_2017[,-1], scale.=FALSE)
plot(pca_votes_2017$x[,1], pca_votes_2017$x[,2], type='n', xlab='PC1', ylab='PC2')
points(pca_votes_2017$x[dem_2017, 1], pca_votes_2017$x[dem_2017, 2], pch=22, bg='blue')
points(pca_votes_2017$x[repub_2017, 1], pca_votes_2017$x[repub_2017, 2], pch=22, bg='red')
  1. 422
  2. 709
../_images/14ef5a21aebebdd80cae3d3e34cdcd4167e40fb1f3f1319a6e2d43427ecd2ab0.png 
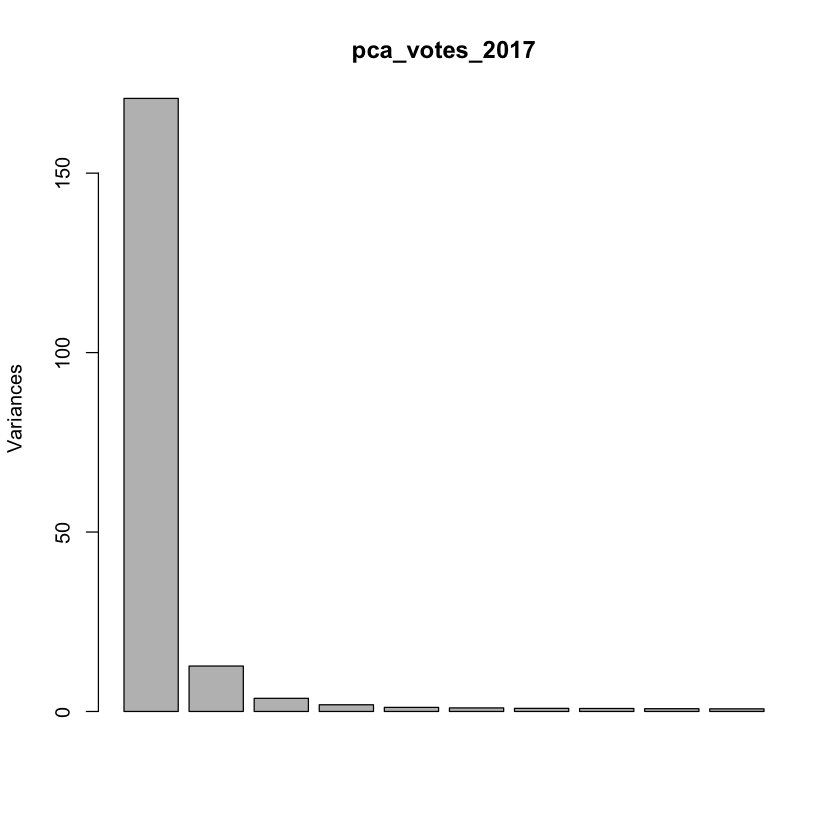
plot(pca_votes_2017)
../_images/86db2243753668fc3d56834a1dc67ce492fbf5510a58c0c509dfd813e815b380.png

Fewer votes (randomly chosen 100 votes)#

set.seed(0)
voting_2017_fewer = voting_2017[,-1]
voting_2017_fewer = voting_2017_fewer[,sample(1:ncol(voting_2017_fewer), 100, replace=FALSE)]
pca_votes_2017_fewer = prcomp(voting_2017_fewer, scale.=FALSE)
plot(pca_votes_2017_fewer$x[,1], pca_votes_2017_fewer$x[,2], type='n', xlab='PC1', ylab='PC2')
points(pca_votes_2017_fewer$x[dem_2017, 1], pca_votes_2017_fewer$x[dem_2017, 2], pch=22, bg='blue')
points(pca_votes_2017_fewer$x[repub_2017, 1], pca_votes_2017_fewer$x[repub_2017, 2], pch=22, bg='red')
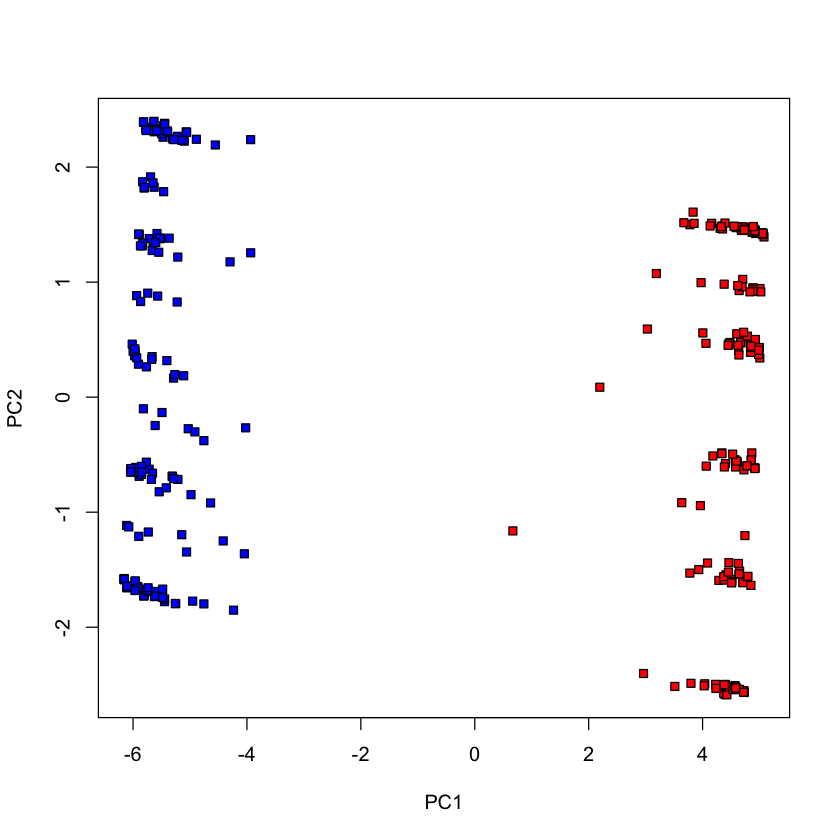
../_images/8a846e86c7408719694dedf169655bef39d2f9398d2603626cd346cf2e4773f0.png

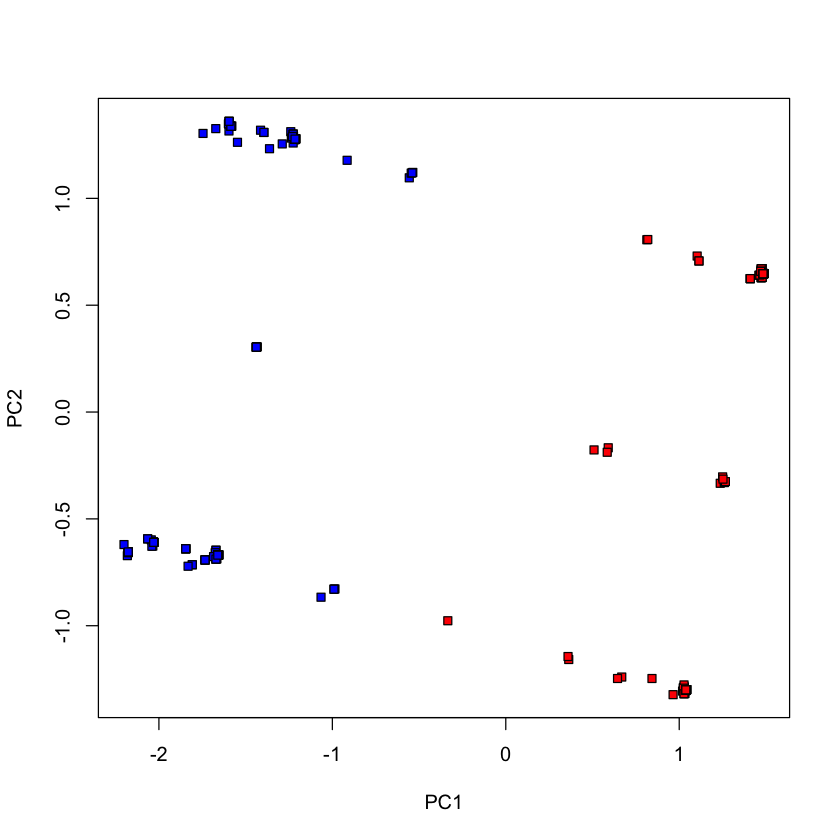
Fewer votes (randomly chosen 20 votes)#

voting_2017_fewer = voting_2017[,-1]
voting_2017_fewer = voting_2017_fewer[,sample(1:ncol(voting_2017_fewer), 20, replace=FALSE)]
pca_votes_2017_fewer = prcomp(voting_2017_fewer, scale.=FALSE)
plot(pca_votes_2017_fewer$x[,1], pca_votes_2017_fewer$x[,2], type='n', xlab='PC1', ylab='PC2')
points(pca_votes_2017_fewer$x[dem_2017, 1], pca_votes_2017_fewer$x[dem_2017, 2], pch=22, bg='blue')
points(pca_votes_2017_fewer$x[repub_2017, 1], pca_votes_2017_fewer$x[repub_2017, 2], pch=22, bg='red')
../_images/ced8381c499938052a3b5557eb86625cf080d7673ba45971ddc53ef761ffe9fd.png

Flow cytometry data#

#| echo: true
flow = read.table('http://www.stanford.edu/class/stats305c/data/sachs.data', sep=' ', header=FALSE)
dim(flow)
plot(prcomp(flow, center=TRUE, scale.=TRUE))
  1. 7466
  2. 11
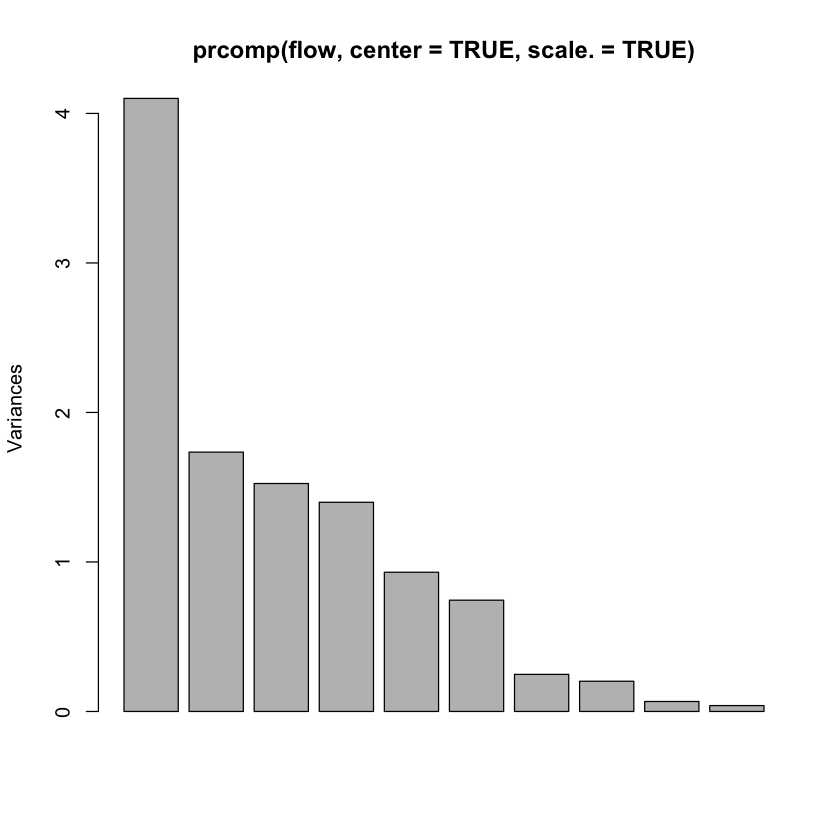
../_images/26c836cefac110c7ee0eb645e72dd5366a10c61765983d32ff3110b156db5193.png

A rank 4 model?#

plot(prcomp(flow, center=TRUE, scale.=FALSE)) # rank 4?
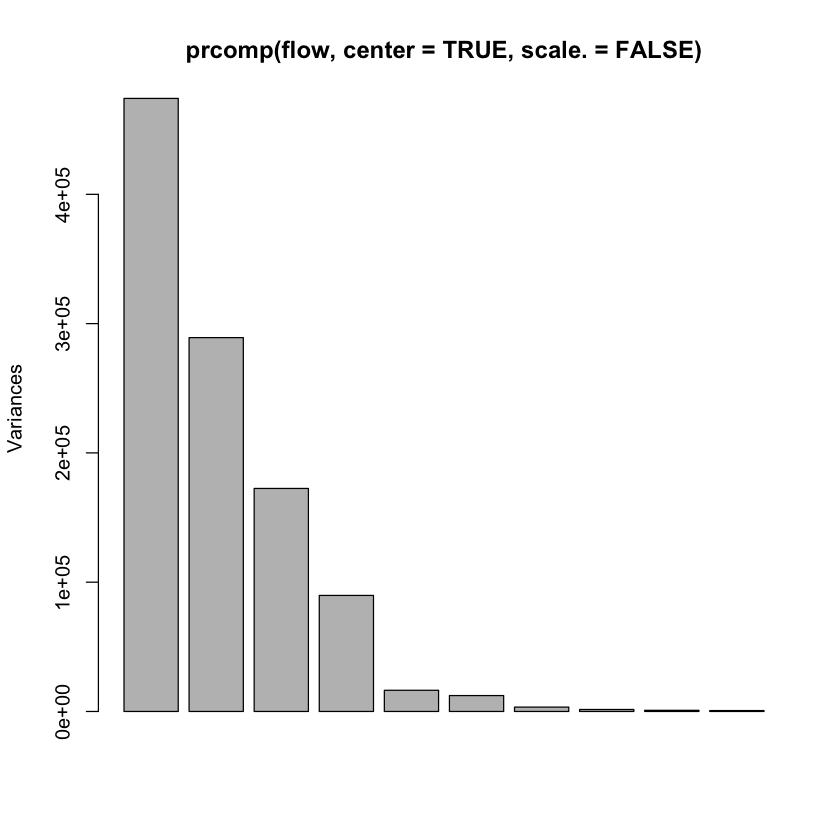
../_images/fb8101a3ae20916b44799b92c6dd408cda54a88b3c916c98c8f359f9d00cac9e.png

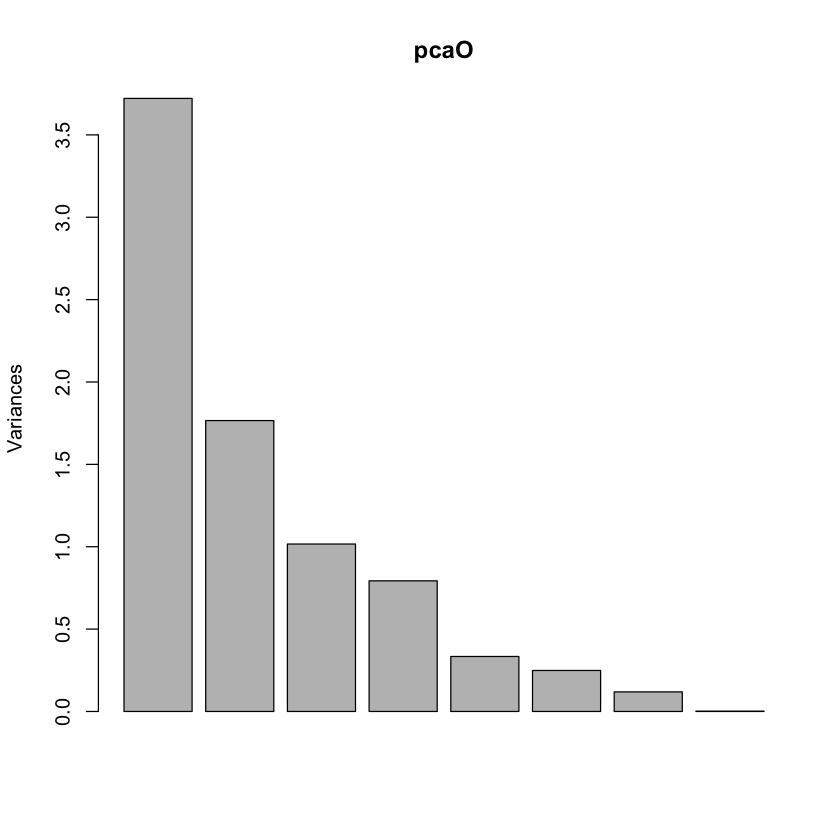
Olive oil data#

#| echo: true
library(pdfCluster)
data(oliveoil)
featO = oliveoil[,3:10]
pcaO = prcomp(featO, scale.=TRUE, center=TRUE)
plot(pcaO)

pdfCluster 1.0-4
../_images/0b163e233b9108bb4609d81ea5780798d8a067adebcc9bbb35f975ba8738bd85.png 
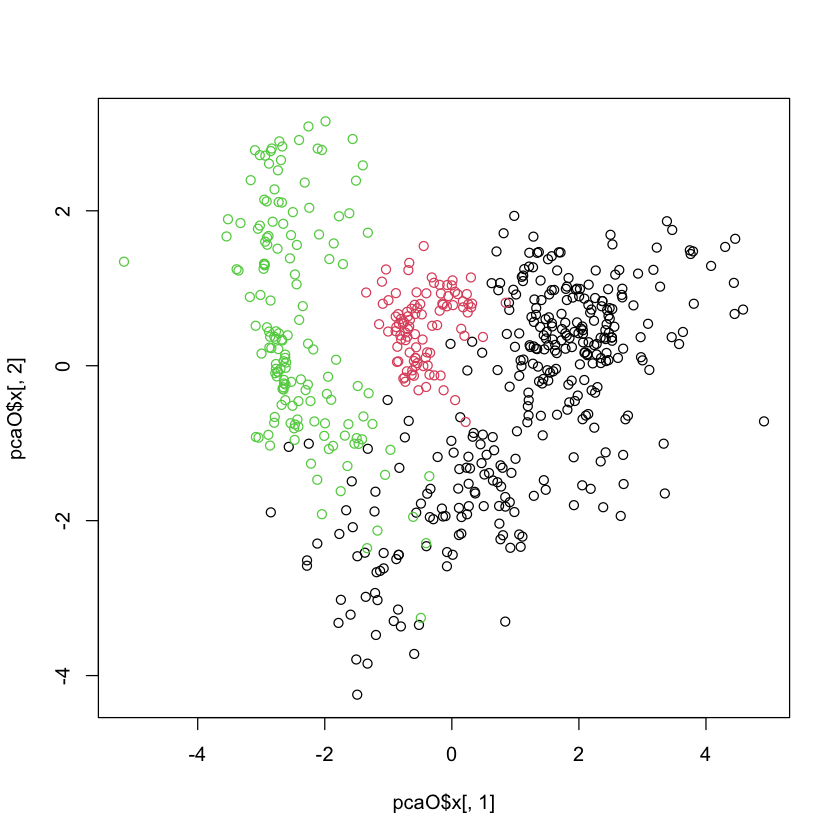
#| echo: true
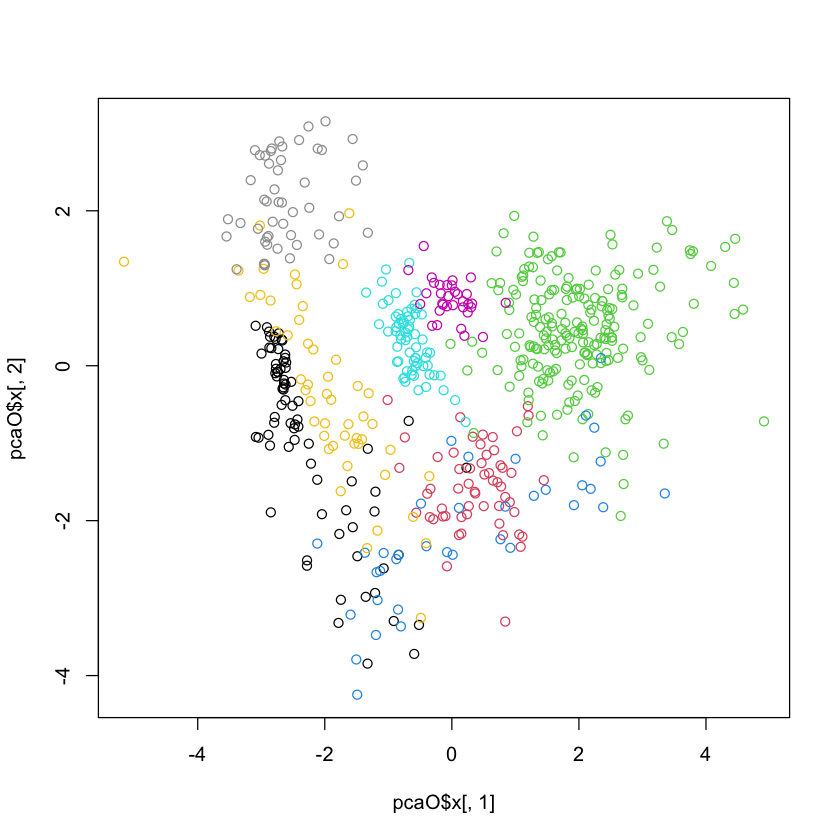
plot(pcaO$x[,1], pcaO$x[,2], col=oliveoil[,'macro.area'])
../_images/c087bf4769f18afa472616f2887b5e2ccf49f11a161708cfe2ad14b9a88657a4.png 
#| echo: true
plot(pcaO$x[,1], pcaO$x[,2], col=oliveoil[,'region'])
../_images/3233f43a6597d6bae41aad760f0e28aa59ecf769ef0a6ee99a0af6239dd50ae4.png
Contents