Ctrl+K

Penalized discriminants

Penalized discriminants#

Download#

Penalized Discriminant Analysis#

Takeaways#

  • Turns regression procedure Y ~ X into a discriminant classifier

    • Y: one-hot encoding of classes

    • X: features

  • Ideal for ridge-type smoothing

Outline#

  • All of multivariate analysis: lm(Y ~ X) and svd()

  • Laplacians and smoothing

  • Most of the time \(Y\), \(X\) will be random vectors rather than data matrices (exceptions will hopefully be clear from context)

Smooth LDA for digits#

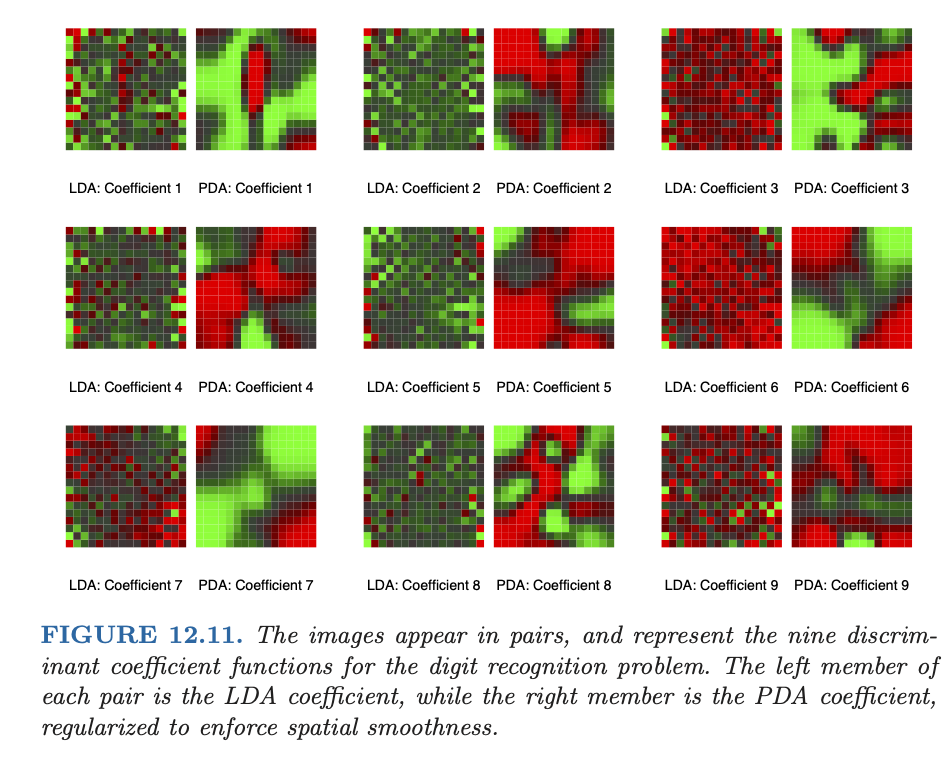
(Source: ESL)

CCA’s generalized eigenvalue problems#

  • In CCA, we looked at eigen-decompositions of

\[ \Sigma_{YY}^{-1/2} \Sigma_{YX} \Sigma_{XX}^{-1} \Sigma_{XY} \Sigma_{YY}^{-1/2} = U_Y \Lambda^2 U_Y' \]

  • Setting \(A_Y'=\Sigma_{YY}^{-1/2}U_Y\) yields solutions

\[ \Sigma_{YX} \Sigma_{XX}^{-1} \Sigma_{XY} a_{Y,i} = \lambda^2_i a_{Y,i}, 1 \leq i \leq m=\text{rank}(\Sigma_{XY}) \]

with

\[ a_{Y,i}'\Sigma_{YY}a_{Y,j} = \delta_{ij}. \]

  • Yielded the canonical variates

\[ Z_{Y,i} = a_{Y,i}'Y, \qquad Z_{Y,i}'Z_{Y,j} = \delta_{ij} \]

Matrix form#

  • For non-singular \(A_X, A_Y\)

\[\begin{split} \begin{aligned} Z_Y &= A_Y Y \\ Z_X &= A_X X \end{aligned} \end{split}\]

Projection version#

  • Let \(P_X, P_Y\) denote the correspond projections (either sample or population) of centered \(X, Y\)

Population version#

  • \(P_X\) projection onto \(\text{span}((X_i - \mathbb{E}[X_i]), 1 \leq i \leq p)\) in \(L^2(\mathbb{P})\)

Sample version#

  • With \(R_C=I-P_C=I-n^{-1}11'\), we see that

\[\hat{P}_X = RX(X'RX)^{-1}X'R\]

projects onto \(\text{span}((X_i - \mathbb{E}[X_i]), 1 \leq i \leq p)\) in \(L^2(\widehat{\mathbb{P}})\)

Canonical variates#

\[ P_XP_Y = \sum_{i=1}^{m} \lambda_i Z_{X,i} Z_{Y,i}' = \sum_{i=1}^m \lambda_i Z_{X,i} \otimes Z_{Y,i}, \qquad m = \text{rank}(\Sigma_{XY}) \]

Regression in terms of canonical variates#

  • Straightforward to check

\[\begin{split} \begin{aligned} \Lambda &= \text{argmin}_{L} \mathbb{E}[\|Z_Y - L'Z_X\|^2_2] \\ \end{aligned} \end{split}\]

  • \(\implies\) \(X\) uses \(\Lambda Z_X\) to predict \(Z_Y\)

  • Given nominal OLS fits \(\hat{Y}=B'X\) (\(B=\Sigma_{XX}^{-1}\Sigma_{XY}\)) we can conclude that \(A_YB'X=A_Y\hat{Y}\) predicts \(Z_Y\).

  • \(\implies\) \(A_YB'X=\Lambda Z_X\)!

Reduced rank regression#

  • Claim:

\[ \text{argmin}_{L: \text{rank}(L)=k} \mathbb{E}[\|Z_Y - L'Z_X\|^2_2] = \text{diag}(\lambda_1, \dots, \lambda_k, 0, \dots, 0) \overset{def}{=} \Lambda_k \]

  • Almost OS of Hastie et al.

Regression in original space#

  • By equivariance of regression

\[ \text{argmin}_B \mathbb{E}[(Y-BX)\Sigma_{YY}^{-1}(Y-BX)] = A_Y^{-1}\Lambda A_X \]

Reduced rank#

\[ \text{argmin}_{B:\text{rank}(B)=k} \mathbb{E}[(Y-BX)\Sigma_{YY}^{-1}(Y-BX)] = A_Y^{-1}\Lambda_k A_X \]

Connection to multivariate linear regression#

  • Consider regression Y ~ X (burying 1 within \(X\))

\[ \mathbb{R}^q \ni Y|X \sim N(B'X, \Sigma) \]

  • Recall the sample quantities

\[\begin{split} \begin{aligned} \textrm{SST}_{q \times q} &= Y^T(I-P_C)Y \\ \textrm{SSE}_{q \times q} &= Y^T(I-P_F)Y \\ \textrm{SSR}_{q \times q} &= Y^T(P_F-P_C)Y \\ &= \hat{Y}'(P_F-P_C)\hat{Y}\\ &= \hat{Y}'(I-P_C)Y\\ \textrm{SST} &= \textrm{SSE}+\textrm{SSR} \end{aligned} \end{split}\]

  • Population quantities

\[\begin{split} \begin{aligned} Q^Y_T &= \mathbb{E}[(Y- \mathbb{E}[Y])(Y- \mathbb{E}[Y])'] \\ Q^Y_E &= \mathbb{E}[(Y- BX)(Y- BX)'] \\ Q^Y_R &= \mathbb{E}[(\mathbb{E}[Y]- BX)(\mathbb{E}[Y]- BX)'] \\ &= \mathbb{E}[(\mathbb{E}[Y]- BX)Y'] \\ \end{aligned} \end{split}\]

CCA eigenvalues and multivariate regression#

  • The generalized eigenvalue problem we considered above is

\[ Q^Y_R v = \lambda^2 Q^Y_T v \]

  • \(\implies\) \(\Lambda^2\) are eigenvalues of \(H(H+E)^{-1}\)

  • Swapping \(X\) and \(Y\) shows these are the same eigenvalues for the regression X ~ Y (with \(Q^X_T, Q^X_E, Q^X_R\))

  • In LDA model X ~ Y really is multivariate linear regression…

So what? (Back to LDA)#

Two key observations (implicit / semi-explicit in ESL)#

  • \(\Sigma_{YY}^{-1/2}Q_R\Sigma_{YY}^{-1/2}= U_Y\Lambda^2 U_Y'\)

  • \(\implies\) we can find \(A_Y=\Sigma_{YY}^{-1/2}U_Y\)

  • Given \(A_Y\) and \(BX\) we can assume \(A_YB'X\) predicts \(A_YY=Z_Y\).

  • Combiined: \(\implies\) \(A_YB'X = \Lambda Z_X, \iff Z_X=\Lambda^{-1}A_YB'X = \Lambda^{-1}A_Y\hat{Y}(X)\)

Fisher’s discriminants from canonical variates#

  • CCA (equivalent) eigenproblems (with \(a_{i,X}'\Sigma_{XX} a_{j,X} = \delta_{ij}\))

\[\begin{split} \begin{aligned} \Sigma_{XX} a_{i,X} &= \lambda_i^2 \Sigma_{XY}\Sigma_{YY}^{-1} \Sigma_{YX} a_{i,X} \\ \Sigma_{X,T} a_{i,X} &= \lambda_i^2 \Sigma_{X,B} a_{i,X} \\ Q^X_T a_{i,X} &= \lambda_i^2 Q^X_R a_{i,X} \\ \end{aligned} \end{split}\]

  • LDA (equivalent) eigenproblems

\[\begin{split} \begin{aligned} \Sigma_{X,W} \alpha_{i,X} &= \bar{\lambda}_i^2 \Sigma_{X,B} \alpha_{i,X} \\ Q^X_E \alpha_{i,X} &= \bar{\lambda}_i^2 Q^X_R \alpha_{i,X} \end{aligned} \end{split}\]

  • Desiderata: find eigenvectors \(\alpha_i\) and normalize \(\alpha_{i,X}'\Sigma_{X,W}\alpha_{j,X} = \delta_{ij}\)

Equivalence of eigenproblems#

Claim#

  • We can take

\[\begin{split} \begin{aligned} \bar{\lambda}_i^2 &= 1 - \lambda_i^2 \\ \alpha_{i,X} &= \frac{1}{\sqrt{1 - \lambda_i^2}}a_{i,X} \\ \end{aligned} \end{split}\]

Proof of claim#

Eigenvalue#

\[ (Q_E + Q_R) a_i = \lambda^2 Q_R a_i \iff Q_E a_i = (1 - \lambda^2) Q_R a_i \]
Aside#

  • \(\implies\) reduced rank regression with \(Q_T\) is equivalent to using \(Q_E\): (c.f. exercise 3.22 of ESL)

Normalization#

\[\begin{split} \begin{aligned} \alpha_i'Q_E\alpha_i &= \frac{1}{1 - \lambda_i^2} \cdot a_i'Q_Ea_i \\ &= \frac{1}{1 - \lambda_i^2} \left(a_i'(Q_R+Q_E)a_i - a_i'Q_Ra_i\right) \\ &= \frac{1}{1 - \lambda_i^2} \left(a_i'Q_Ta_i - a_i'Q_Ra_i\right) \\ &= \frac{1}{1 - \lambda_i^2} \left(a_i'Q_Ra_i - \lambda_i^2 a_i'Q_Ta_i\right) \\ &= 1 \end{aligned} \end{split}\]

Sample version (almost)#

  • For one-hot data Y, fit lm(Y ~ X) and form Y_hat = predict(X)

  • Compute

\[ \text{SSR} = Y'\hat{Y} - n \hat{\pi} \hat{pi}' \]

  • Compute eigendecomposition

\[ (\text{SST}/n)^{-1/2}( \text{SSR}/n)(\text{SST}/n)^{-1/2} = \hat{U}_Y \hat{\Lambda}^2 \hat{U}_Y' \]

  • Set \(\hat{A}_Y = (\text{SST}/n)^{-1/2} \hat{U}_Y\) and adjusted fits \(\hat{Y}\hat{A}_Y'\).

  • Matrix of discriminant scores are

\[ \hat{V} = \hat{Y}\hat{A}_Y'(\hat{\Lambda}^2 (I-\hat{\Lambda}^2))^{-1/2} \]

  • Reduced rank LDA: just use first \(k\) of the \(\hat{V}\)’s

Why almost?#

  • For Y, the matrix \(\text{SST}\) is rank-deficient as \(1'Y=1\) for one-hot data

  • \(\implies \hat{\pi} \in \text{null(SST)}...\)

Solution#

  • Take \(\Theta_{K-1 \times K}\) whose column space is \(\text{row(SST)}\) with normalization

\[ \Theta'(D_{\hat{\pi}} - \hat{\pi}\hat{\pi}')\Theta = \Theta'D_{\hat{\pi}}\Theta = I_{K-1} \]

  • Run the above procedure on Y @ Theta.T

This is genius!#

Algorithm#

def fit(self, X, Y):
    self.reg_estimator.fit(X, Y)
    self.A_Y, self.L = solve_eigenproblem(Y, self.reg_estimator.predict(X))
    Z = self.transform(X)
    self.centroids = class_average(Z, Y)
    return self

def transform(self, x_new)
    yhat_new = self.reg_estimator.predict(x_new)
    return (yhat_new @ self.A_Y.T / np.sqrt(L**2 * (1 - L**2))[None,:])[:,:self.rank]

def predict(self, x_new):
    V_new = self.transform(x_new)
    return np.argmin(distance(V_new, centroids), axis=1)

A pause#

  • Relied on (generalized) eigen decomposition of \(Y'\hat{Y}\)

  • This will be fine for (symmetric) linear estimators like ridge

\[ \hat{Y} = X(X'X + \gamma \cdot I)^{-1}X'Y = S_{\gamma}(Y) \]

  • Easy to generalize this with a basis expansion

\[ \hat{Y} = h(X)(h(X)'h(X) + \gamma \cdot Q)^{-1} h(X)'Y \]

What does it all mean?#

  • We motivated / derived the algorithm for lm(Y ~ X)…

  • For ridge, simply replace \(\Sigma_{XX}=\Sigma_{XX} + \gamma \cdot I\) above

  • Corresponds to regularized CCA

\[ \text{maximize}_{a_Y, a_X: a_Y'\Sigma_{YY}a_Y \leq 1, a_X'(\Sigma_{XX} + \gamma \cdot I) a_X \leq 1} a_Y'\Sigma_{YX}a_X \]

  • \(\implies\) resulting \(Z_X\)’s are regularized canonical variates as are discriminants \(V\).

Back to the digits#

Laplacian smoothing#

  • The application used in ESL and Hastie, Buja, Tibshirani (1995) considers features that are \(16 \times 16\) grayscale images.

  • Given an undirected graph \(G=(V,E)\) (like the \(16 \times 16\) lattice in 2D), define the difference operator (after orienting edges) \(D:\mathbb{R}^V \to \mathbb{R}^E\)

\[ Df_e = Df_{[v_1,v_2]} = f_{v_2} - f_{v_1} \]

  • The Laplacian (non-negative definite version) is the map \(\Delta: \mathbb{R}^V \times \mathbb{R}^V\)

\[ (\Delta f)_i = (D^*D f)_i = \sum_{e:v_1=j,v_2=i} f_i - f_j \]

  • Regression problem: for digit \(d\), \(X\) the stack of images

\[ \hat{\beta}_d = (X'X + \lambda \Delta)^{-1} X'Y_d \]

Degrees of freedom#

  • For a (usually symmetric) linear smoother \(S:\mathbb{R}^n \to \mathbb{R}^n\)

\[ df(S) = \text{Tr}(S). \]

  • Chosen to be about 40 for each digit \(d\).

Laplacian and manifold learning#

  • Early 2000s saw an explosion in interest in Laplacians

  • Given noisy \(W = \mu + \epsilon \in \mathbb{R}^V\) can smooth

\[ \hat{\mu} = (I + \lambda \Delta)^{-1} W = \text{argmin}_{\mu} \|\mu - W\|^2_{\mathbb{R}^V} + \lambda \cdot \mu'\Delta \mu \]

  • Prior variance is \(\Delta^{\dagger}\) (not invertible as \(\Delta 1=0\)): \(\implies\) more weight on functions with small eigenvalues

Intuition from Laplacian on \(\mathbb{R}^k\)#

  • For \(f \in \mathbb{C}^2(\mathbb{R}^k)\)

\[ (\Delta f)(x) = - \sum_{j=1}^k \frac{\partial^2f}{\partial^2 x_i}(x) \]

Eigenfunctions#

\[ \Delta (\sin(\lambda'x)) = \|\lambda\|^2 \sin(\lambda'x) \]

  • Functions with small eigenvalues are smoother than higher eigenvalues…

Generalizations#

  • Take \(\alpha: [0,\infty) \to [0, \infty)\) and consider

\[ \hat{\mu}_{\alpha} = \text{argmin}_{\mu} \|\mu - W\|^2_{\mathbb{R}^V} + \lambda \cdot \mu'\alpha(\Delta) \mu \]

  • Easy to apply given eigen decomposition of \(\Delta\)

  • Graph Neural Net: for graph-based features, parameterize / learn \(\alpha\)

Generators#

  • Taking \(\alpha(v)=v\), \(\Delta\) is (discrete-time) generator of random walk on the graph…

  • Taking \(\alpha(v)=e^{-tv}\), \(e^{-t\Delta}\) is the transition kernel for continuous-time random walk…

  • In Euclidean space \(e^{-t\Delta}\) forms the transition probabilities for Brownian motion…

\[\begin{split} \begin{aligned} (e^{-t\Delta}f)(x) &= (2\pi)^{-k/2} \int_{\mathbb{R}^k} e^{-\frac{t}{2}\|y-x\|^2_2} f(y) \; dy \\ &= \mathbb{E}[f(B_t)|B_0=x] \end{aligned} \end{split}\]

Niyogi and Belkin (2001)#

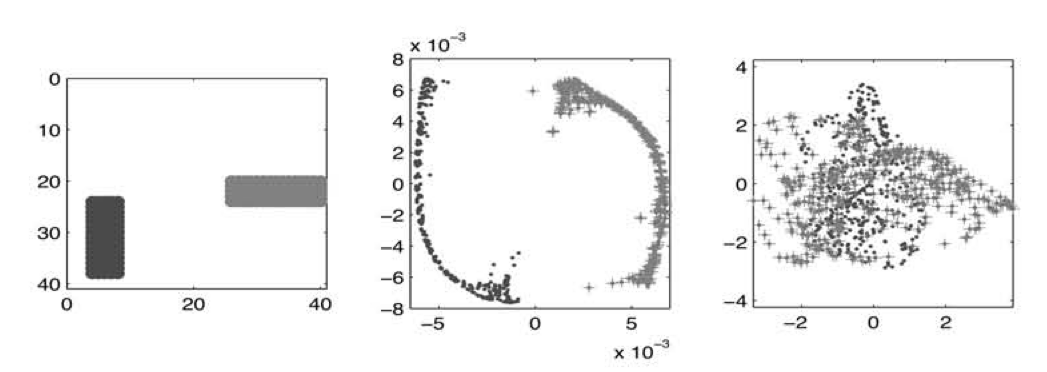
  • Laplacian embedding better than PCA!

Laplacian embedding#

Rough description#

  • Given samples \(X_i, 1 \leq i \leq n\) in some metric space \((T, d)\), construct a graph \(G_n\) with Laplacian \(\Delta_n\)

  • Compute low-rank eigen decomposition (of smallest eigenfunctions!)

\[ \Delta_n = L_n \Lambda_n^{-1} L_n' \]

  • “Embed” in \(\mathbb{R}^k\) for some user chosen rank \(k\):

\[ E^k_{n} = L_n \sqrt{\Lambda_n} \]

  • At least locally, we hope (?)

\[ \|E^k_{n,i} - E^k_{n,j}\|_2 \approx d(X_i, X_j) \]

  • A version of kernel PCA (with data-dependent kernel)

Why do we hope?#

  • Suppose \(T\) is a Riemannian manifold \((M,g)\) that is densely sampled by the empirical measure \(\hat{\mathbb{P}}\)

  • Maybe \(\hat{\mathbb{P}}\) is close to Riemannian measure \(\mu\)

  • We hope \(L_n\) “look like” eigenfunctions of Laplacian associated to \((M,g)\)

\[ \Delta f = \lambda f, \qquad f \in L^2(\mu) \]

  • Why do we care about \(x \mapsto (\lambda_i^{-1/2} f_i(x))_{1 \leq i \leq k} = E_k(x)\)?

A kernel of hope#

  • Consider

\[ {\cal H}_{\alpha} = \left\{f: f \in L^2(\mu): \langle f, \alpha(\Delta) f \rangle_{L^2(\mu)} < \infty\right\} \]

  • For appropriate choices of \(\alpha\), \({\cal H}_{\alpha}\) is an RKHS! (c.f. Sobolev embedding)

  • Set

\[ E_k(x) = \sum_{i=1}^k \alpha(\lambda_i)^{-1/2} f_i(x) \]

  • And…

\[ \|E_k(x) - E_k(y)\|^2_{\mathbb{R}^k} \overset{k \to \infty}{\to} K_{\alpha}(x,y) \]

  • Fact: given any covariance kernel \(K:T \times T \to \mathbb{R}\), the map \(d(x,y) = \|K_x-K_y\|_{\cal H}\) is a (pseudo-metric) on \(T\)…

  • \(\implies\) if \(d^2(x,y) = \|K_{\alpha}(x) - K_{\alpha}(y)\|^2_{\cal H}\) then \(E_k\) are approximate embeddings…

  • This assumption implies our metric was Euclidean (in some asymptotic sense). Not all metrics are Euclidean…

  • Related differential geometry: Spectral geometry

Contents