Multivariate regression#
Download#
Multiple linear regression#
Response matrix: \(Y \in \mathbb{R}^{n \times q}\)
Design matrix: \(X \in \mathbb{R}^{n \times p}\)
MKB swaps \(p\) and \(q\). Here \(p\) always refers to features.
Model#
\[
Y_{n \times q} = X_{n \times p} B_{p \times q} + \epsilon_{n \times q}, \qquad \epsilon \sim N(0, I_{n \times n} \otimes \Sigma_{q \times q})
\]
MKB uses \(U\) instead of \(\epsilon\).
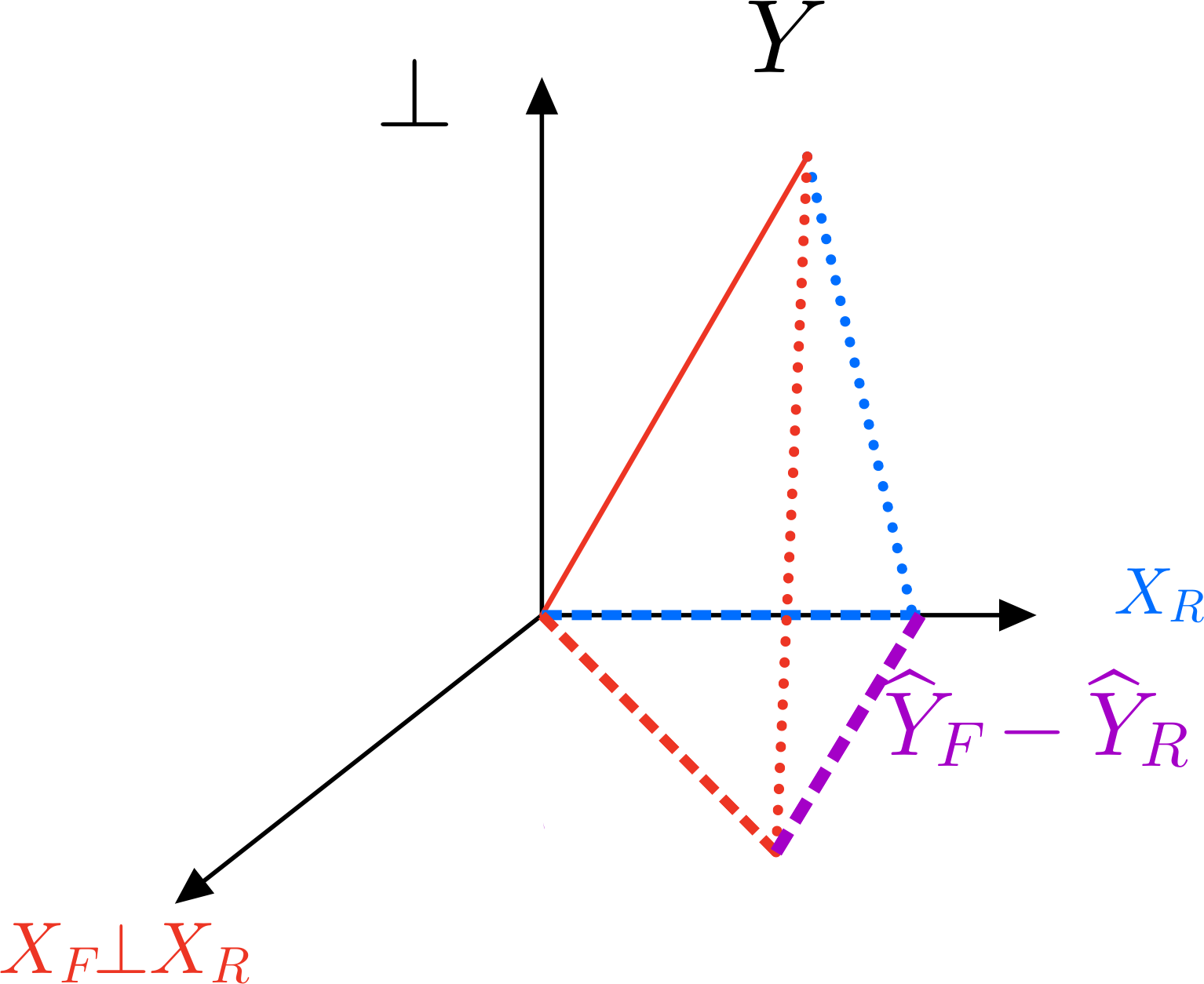
Geometry of OLS still applies#
Soils example#
library(car)
data(Soils)
str(Soils)
Loading required package: carData
'data.frame': 48 obs. of 14 variables:
$ Group : Factor w/ 12 levels "1","2","3","4",..: 1 1 1 1 2 2 2 2 3 3 ...
$ Contour: Factor w/ 3 levels "Depression","Slope",..: 3 3 3 3 3 3 3 3 3 3 ...
$ Depth : Factor w/ 4 levels "0-10","10-30",..: 1 1 1 1 2 2 2 2 3 3 ...
$ Gp : Factor w/ 12 levels "D0","D1","D3",..: 9 9 9 9 10 10 10 10 11 11 ...
$ Block : Factor w/ 4 levels "1","2","3","4": 1 2 3 4 1 2 3 4 1 2 ...
$ pH : num 5.4 5.65 5.14 5.14 5.14 5.1 4.7 4.46 4.37 4.39 ...
$ N : num 0.188 0.165 0.26 0.169 0.164 0.094 0.1 0.112 0.112 0.058 ...
$ Dens : num 0.92 1.04 0.95 1.1 1.12 1.22 1.52 1.47 1.07 1.54 ...
$ P : int 215 208 300 248 174 129 117 170 121 115 ...
$ Ca : num 16.4 12.2 13 11.9 14.2 ...
$ Mg : num 7.65 5.15 5.68 7.88 8.12 ...
$ K : num 0.72 0.71 0.68 1.09 0.7 0.81 0.39 0.7 0.74 0.77 ...
$ Na : num 1.14 0.94 0.6 1.01 2.17 2.67 3.32 3.76 5.74 5.85 ...
$ Conduc : num 1.09 1.35 1.41 1.64 1.85 3.18 4.16 5.14 5.73 6.45 ...
Estimation of \(B\)#
Negative log-likelihood#
\[\begin{split}
\begin{aligned}
\ell(B,\Sigma) &= - \log L(B,\Sigma|X,Y) \\
&= \frac{n}{2} \log |2\pi\Sigma| + \frac{1}{2} \text{Tr}\left(\Sigma^{-1}(Y-XB)^T(Y-XB)\right) \\
\end{aligned}
\end{split}\]
As in one-sample problem
\[
\frac{1}{t}\left[ \ell(B + t\Delta,\Sigma) - \ell(B, \Sigma) \right] = \frac{1}{2}\text{Tr}\left(\Sigma^{-1} \left(\Delta^TX^T(Y-XB) + (Y-XB)^TX\Delta \right) \right) + O(t^2)
\]
Score equation (assuming \(\Sigma >0\))
\[
X^T(Y-X\hat{B}) = 0 \qquad \implies \hat{B} = (X^TX)^{-1}X^TY \in \mathbb{R}^{p \times q}
\]
Estimation of \(\Sigma\)#
\[
\hat{\Sigma}_{MLE} = \frac{1}{n}Y^T(I-P_F)Y, \qquad P_F = X(X^TX)^{-1}X^T
\]
For \(\hat{\Sigma}_{MLE}>0\) we need \(\text{rank}(I-P_F) \geq q\) which is generic if \(n-p \geq q\).
Unbiased estimate#
\[
\hat{\Sigma} = \frac{1}{n-p} Y^T(I-P_F)Y
\]
Minimized (negative) log-likelihood#
As in one-sample problem we see
\[
\ell(\hat{B}, \hat{\Sigma}_{MLE}) = \frac{n}{2} \log \det(2\pi\hat{\Sigma}) + \frac{n}{2}
\]
Criterion for use e.g. in AIC, BIC…
LRT (up to multiplicative factor)#
\[
\log \det(\hat{\Sigma}_R^{-1} \hat{\Sigma}_F)
\]
Distribution results#
Fairly easy to check:
\(\hat{B} \sim N(B, (X^TX)^{-1} \otimes \Sigma)\)
\((n-p) \hat{\Sigma} \sim \text{Wishart}(n-p, \Sigma)\)
\(\hat{B}\) independent of \(\hat{\Sigma}\)
Sums of squares matrices#
Set \(I-P_C=I-\frac{1}{n}11^T\).
Just like
lmbut matrices…
\[\begin{split}
\begin{aligned}
\textrm{SST}_{q \times q} &= Y^T(I-P_C)Y \\
\textrm{SSE}_{q \times q} &= Y^T(I-P_F)Y \\
\textrm{SSR}_{q \times q} &= Y^T(P_F-P_C)Y \\
\textrm{SST} &= \textrm{SSE}+\textrm{SSR}
\end{aligned}
\end{split}\]
Analogy of \(F\)-test in summary.lm#
Typically first column of \(X\) is \(1\).
Usual \(F\) test is of
\[
H_0: E[Y|X] = 1\mu^T
\]
Natural matrix to consider
\[
HE^{-1} \qquad H=\textrm{SSR}, \qquad E=\textrm{SSE}
\]
Likelihood ratio test statistic#
\[
\log\det( \textrm{SST}^{-1}\; \textrm{SSE}) = - \log \det((H + E)^{-1}E)
\]
Test statistic: Wilks’ Lambda (LRT/n), Roy’s maximum root: largest eigenvalue, etc.
Section 6.5.4. MKB use \((H+E)^{-1}E\) as analog of \(1-R^2\): a Beta matrix under \(H_0\)
Inference#
General linear hypothesis#
\[
H_0:C_{r \times p} B_{p \times q} A_{q \times c} = h_{r \times c}
\]
Special case#
To test hypotheses of the form
\[
H_0:CB=0
\]
Key quantities are sums of squares matrices
\[\begin{split}
\begin{aligned}
H &= SSE(R) - SSE(F) \\ &= Y^T(P_F-P_R)Y\\
E &= SSE(F) \\ &= Y^T(I-P_F)Y\\
\end{aligned}
\end{split}\]
with
\[
P_F-P_R = X(X^TX)^{-1}C^T(C(X^TX)^{-1}C^T)^{-1}C(X^TX)^{-1}X^T
\]
Where does \(P_F-P_R\) come from?#
Type III MANOVA#
#| echo: true
soils.full = lm(cbind(pH, N, Dens, P, Ca, Mg, K, Na, Conduc) ~
Block + Contour * Depth,
data=Soils)
Manova(soils.full, test.statistic="Wilks", type=3)
Type III MANOVA Tests: Wilks test statistic
Df test stat approx F num Df den Df Pr(>F)
(Intercept) 1 0.006336 435.63 9 25.000 < 2.2e-16 ***
Block 3 0.079430 3.77 27 73.655 3.347e-06 ***
Contour 2 0.159872 4.17 18 50.000 3.246e-05 ***
Depth 3 0.028896 6.45 27 73.655 9.554e-11 ***
Contour:Depth 6 0.216611 0.86 54 132.070 0.7392
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Sanity check for Block#
## Response matrix
Y = with(Soils, cbind(pH, N, Dens, P, Ca, Mg, K, Na, Conduc))
## Projection for full model
X_F = model.matrix(soils.full)
P_F = X_F %*% solve(t(X_F) %*% X_F) %*% t(X_F)
## Projection for reduced model
soils.red = lm(cbind(pH, N, Dens, P, Ca, Mg, K, Na, Conduc) ~ Contour * Depth,
data=Soils)
X_R = model.matrix(soils.red)
P_R = X_R %*% solve(t(X_R) %*% X_R) %*% t(X_R)
Compute the LRT#
E = t(Y) %*% (diag(rep(1, nrow(Y))) - P_F) %*% Y
H = t(Y) %*% (P_F - P_R) %*% Y
wilks = det(E %*% solve(E + H))
c(wilks=wilks)
Manova(soils.full, test.statistic="Wilks", type=3)
wilks: 0.0794302001416677
Type III MANOVA Tests: Wilks test statistic
Df test stat approx F num Df den Df Pr(>F)
(Intercept) 1 0.006336 435.63 9 25.000 < 2.2e-16 ***
Block 3 0.079430 3.77 27 73.655 3.347e-06 ***
Contour 2 0.159872 4.17 18 50.000 3.246e-05 ***
Depth 3 0.028896 6.45 27 73.655 9.554e-11 ***
Contour:Depth 6 0.216611 0.86 54 132.070 0.7392
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Types of Sums of Squares#
Here is a good reference
For \(q=1\),
Rreturns Type I sums of squares. Arguably, Type II or III is more natural.When no interactions present, Type II will agree with Type III, otherwise can differ: see
DepthandContourbelow.When designs are balanced, Type I can agree with Type II.
# Look at rows for `Depth`
Manova(soils.full, test.statistic="Wilks", type=3) # compare to type=2
Type III MANOVA Tests: Wilks test statistic
Df test stat approx F num Df den Df Pr(>F)
(Intercept) 1 0.006336 435.63 9 25.000 < 2.2e-16 ***
Block 3 0.079430 3.77 27 73.655 3.347e-06 ***
Contour 2 0.159872 4.17 18 50.000 3.246e-05 ***
Depth 3 0.028896 6.45 27 73.655 9.554e-11 ***
Contour:Depth 6 0.216611 0.86 54 132.070 0.7392
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Type I vs. Type 2 & 3#
X = rnorm(50)
W = rnorm(50)
Z = matrix(rnorm(100), 50, 2)
anova(lm(Z ~ X + W))
Manova(lm(Z ~ X + W), type=2)
Manova(lm(Z ~ X + W), type=3)
| Df | Pillai | approx F | num Df | den Df | Pr(>F) | |
|---|---|---|---|---|---|---|
| <int> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| (Intercept) | 1 | 0.131648226 | 3.486961 | 2 | 46 | 0.038904605 |
| X | 1 | 0.185791947 | 5.248308 | 2 | 46 | 0.008849405 |
| W | 1 | 0.008329814 | 0.193195 | 2 | 46 | 0.824986612 |
| Residuals | 47 | NA | NA | NA | NA | NA |
Type II MANOVA Tests: Pillai test statistic
Df test stat approx F num Df den Df Pr(>F)
X 1 0.18490 5.2173 2 46 0.009076 **
W 1 0.00833 0.1932 2 46 0.824987
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Type III MANOVA Tests: Pillai test statistic
Df test stat approx F num Df den Df Pr(>F)
(Intercept) 1 0.086252 2.1711 2 46 0.125606
X 1 0.184897 5.2173 2 46 0.009076 **
W 1 0.008330 0.1932 2 46 0.824987
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Other test statistics: Roy’s maximum root#
Based on the union-intersection principle using the family
\[\begin{split}
\begin{aligned}
H_{0,a}&: CBa = 0 \\
H_0 &= \cap_{a} H_{0,a}
\end{aligned}
\end{split}\]
For each \(a\) we can test \(H_{0,a}\) with an \(F\)-test
\[
\frac{1}{k a^TEa / (n-p)}(C\widehat{B}a)^T \left(C(X^TX)^{-1}C^T \right)^{-1} C\widehat{B}a = \frac{n-p}{k} \frac{a^THa}{a^TEa}
\]
Ignoring factor \((n-p)/k\) we then maximize over \(a\)
\[\begin{split}
\begin{aligned}
\sup_a \frac{a^THa}{a^TEa} &= \sup_b \frac{b^TE^{-1/2}HE^{-1/2}b}{b^Tb} \\
&= \lambda_1(HE^{-1})
\end{aligned}
\end{split}\]
Computing Roy’s maximum root#
#| echo: true
eigvals = as.numeric(eigen(H %*% solve(E))$values)
roy = max(eigvals); roy
Manova(soils.full, test.statistic="Roy", type=3)
Warning message:
“imaginary parts discarded in coercion”
2.21913569998462
Type III MANOVA Tests: Roy test statistic
Df test stat approx F num Df den Df Pr(>F)
(Intercept) 1 156.827 435.63 9 25 < 2.2e-16 ***
Block 3 2.219 6.66 9 27 5.625e-05 ***
Contour 2 2.705 7.82 9 26 1.739e-05 ***
Depth 3 14.251 42.75 9 27 1.126e-13 ***
Contour:Depth 6 0.902 3.01 9 30 0.01113 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Hotelling-Lawley trace#
Test statistic: \(\text{Tr}(HE^{-1})\).
lawley = sum(eigvals)
c(lawley=lawley)
Manova(soils.full, test.statistic="Hotelling-Lawley", type=3)
lawley: 4.18307516301549
Type III MANOVA Tests: Hotelling-Lawley test statistic
Df test stat approx F num Df den Df Pr(>F)
(Intercept) 1 156.827 435.63 9 25 < 2.2e-16 ***
Block 3 4.183 3.67 27 71 6.188e-06 ***
Contour 2 3.394 4.52 18 48 1.443e-05 ***
Depth 3 15.480 13.57 27 71 < 2.2e-16 ***
Contour:Depth 6 1.954 0.84 54 140 0.7585
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Pillai-Bartlett trace#
Test statistic: \(\text{Tr}((I + HE^{-1})^{-1})) = \text{Tr}(E(E+H)^{-1}).\)
pillai = sum(eigvals / (1 + eigvals))
c(pillai=pillai)
Manova(soils.full, test.statistic="Pillai", type=3)
pillai: 1.67579179706467
Type III MANOVA Tests: Pillai test statistic
Df test stat approx F num Df den Df Pr(>F)
(Intercept) 1 0.99366 435.63 9 25 < 2.2e-16 ***
Block 3 1.67579 3.80 27 81 1.777e-06 ***
Contour 2 1.13773 3.81 18 52 8.025e-05 ***
Depth 3 1.51137 3.05 27 81 6.020e-05 ***
Contour:Depth 6 1.23510 0.86 54 180 0.7311
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Finding Sum of Squares from Manova#
M = Manova(soils.full)
sqrt(sum((M$SSPE - E)^2))
sqrt(sum((M$SSP$Block - H)^2))
3.05837818231743e-09
2.65808234525054e-09
Tests about different responses#
We might sometimes be interested in testing a hypothesis of the form
\[
H_0: BM = 0
\]
For example, the hypothesis that all \(q\) coefficient vectors are identical
\[
H_0: B = \gamma 1^T \quad \iff \quad B\left(I - \frac{1}{q} 11^T \right) = 0
\]
Reduced response#
In this case, we use response vector \(\widetilde{Y}=YM\) and the model
\[
\widetilde{Y} = X\widetilde{B} + \widetilde{\epsilon}
\]
Our hypothesis here can be expressed as \(\widetilde{B}=0\).
Hence, the relevant sums of squares are
\[\begin{split}
\begin{aligned}
\tilde{H} &= (YM)^TP_FYM
\tilde{E} &= (YM)^T(I-P_F)YM \\
\end{aligned}
\end{split}\]
q = ncol(Y)
M = (diag(rep(1, q)) - matrix(1, q, q) / q)[,1:(q-1)]
E_new = t(M) %*% E %*% M
H_new = t(M) %*% (t(Y) %*% Y - E) %*% M
roy = max(as.numeric(eigen(H_new %*% solve(E_new))$values)); roy
1849.92657346278
Combining both types of tests#
To test \(H_0: CBM=0\), we use
\[\begin{split}
\begin{aligned}
H &= (YM)^T(P_F-P_R)YM \\
E &= (YM)^T(I-P_F)YM \\
\end{aligned}
\end{split}\]
Affine shifts#
Finally, suppose \(h \neq 0\)
For this, take any fixed \(B_0 \in H_0\) such that \(CB_0M=h\) and set
\[
\widetilde{Y} = Y - XB_0 | X \sim N(X(B-B_0), I \otimes \Sigma) = N(X\Delta, I \otimes \Sigma)
\]
with \(\Delta=B-B_0\).
Our null is now \(H_0:C\Delta M=0\) and we can use
\[\begin{split}
\begin{aligned}
H &= (\widetilde{Y}M)^T(P_F-P_R)\widetilde{Y}M \\
E &= (\widetilde{Y}M)^T(I-P_F)\widetilde{Y}M \\
\end{aligned}
\end{split}\]