Multiple Linear Regression Inference

Multiple Linear Regression Inference#

Download#

Outline#

Case studies:

A. Galileo’s falling bodies

B. Energy costs of echolocation

Energy costs of echolocation#

url = 'https://raw.githubusercontent.com/StanfordStatistics/stats191-data/main/Sleuth3/bats_energy.csv'
bats = read.table(url, sep=',', header=TRUE)
bats

A data.frame: 20 × 3
Mass	Type	Energy
<dbl>	<chr>	<dbl>
779.0	non-echolocating bats	43.70
628.0	non-echolocating bats	34.80
258.0	non-echolocating bats	23.30
315.0	non-echolocating bats	22.40
24.3	non-echolocating birds	2.46
35.0	non-echolocating birds	3.93
72.8	non-echolocating birds	9.15
120.0	non-echolocating birds	13.80
213.0	non-echolocating birds	14.60
275.0	non-echolocating birds	22.80
370.0	non-echolocating birds	26.20
384.0	non-echolocating birds	25.90
442.0	non-echolocating birds	29.50
412.0	non-echolocating birds	43.70
330.0	non-echolocating birds	34.00
480.0	non-echolocating birds	27.80
93.0	echolocating bats	8.83
8.0	echolocating bats	1.35
6.7	echolocating bats	1.12
7.7	echolocating bats	1.02

Fitting a model#

bats.lm = lm(Energy ~ Type + Mass, data=bats)
summary(bats.lm)

Call:
lm(formula = Energy ~ Type + Mass, data = bats)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.8198 -3.6711 -0.9508  1.1499 13.9899 

Coefficients:
                           Estimate Std. Error t value Pr(>|t|)    
(Intercept)                1.421257   2.660684   0.534    0.601    
Typenon-echolocating bats  1.168512   5.145112   0.227    0.823    
Typenon-echolocating birds 4.600720   3.537113   1.301    0.212    
Mass                       0.057495   0.007557   7.608 1.06e-06 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.303 on 16 degrees of freedom
Multiple R-squared:  0.8791,	Adjusted R-squared:  0.8565 
F-statistic: 38.79 on 3 and 16 DF,  p-value: 1.437e-07

Other models#

simpler.lm = lm(Energy ~ Type, data=bats)
coef(simpler.lm)

(Intercept): 3.07999999999999
Typenon-echolocating bats: 27.97
Typenon-echolocating birds: 18.0733333333333

complex.lm = lm(Energy ~ Type + Mass + Type:Mass, data=bats)
coef(complex.lm)

(Intercept): 0.493983042663024
Typenon-echolocating bats: 10.7334006739125
Typenon-echolocating birds: 2.82275854753212
Mass: 0.0896366363028415
Typenon-echolocating bats:Mass: -0.0495909468413778
Typenon-echolocating birds:Mass: -0.021861993030729

Case study B: Galileo’s data#

url = 'https://raw.githubusercontent.com/StanfordStatistics/stats191-data/main/Sleuth3/galileo.csv'
galileo = read.table(url, sep=',', header=TRUE)
with(galileo, plot(Height, Distance))

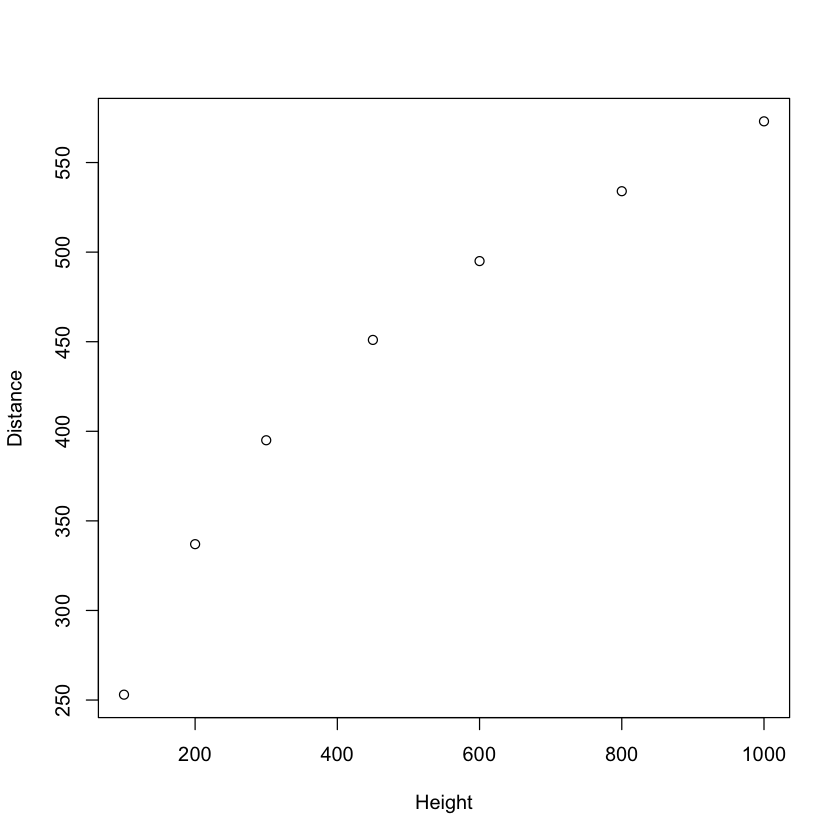
../../_images/0a1896ed9c06a14ac4efd11f71da49599d90bab26cf31455e5d9fe4424a04950.png

Galileo fit a quadratic model to his data
Note the notation I(Height^2) – without I a quadratic term will not be added…

galileo1.lm = lm(Distance ~ Height + I(Height^2), data=galileo)
summary(galileo1.lm)

Call:
lm(formula = Distance ~ Height + I(Height^2), data = galileo)

Residuals:
      1       2       3       4       5       6       7 
-14.308   9.170  13.523   1.940  -6.177 -12.607   8.458 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.999e+02  1.676e+01  11.928 0.000283 ***
Height       7.083e-01  7.482e-02   9.467 0.000695 ***
I(Height^2) -3.437e-04  6.678e-05  -5.147 0.006760 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 13.64 on 4 degrees of freedom
Multiple R-squared:  0.9903,	Adjusted R-squared:  0.9855 
F-statistic:   205 on 2 and 4 DF,  p-value: 9.333e-05

A different way to fit the model

galileo2.lm = lm(Distance ~ poly(Height, 2), data=galileo)
summary(galileo2.lm)

Call:
lm(formula = Distance ~ poly(Height, 2), data = galileo)

Residuals:
      1       2       3       4       5       6       7 
-14.308   9.170  13.523   1.940  -6.177 -12.607   8.458 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)       434.000      5.155  84.190 1.19e-07 ***
poly(Height, 2)1  267.116     13.639  19.585 4.01e-05 ***
poly(Height, 2)2  -70.194     13.639  -5.147  0.00676 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 13.64 on 4 degrees of freedom
Multiple R-squared:  0.9903,	Adjusted R-squared:  0.9855 
F-statistic:   205 on 2 and 4 DF,  p-value: 9.333e-05

Predictions / CIs are the same

predict(galileo1.lm, list(Height=250), interval='confidence')
predict(galileo2.lm, list(Height=250), interval='confidence')

A matrix: 1 × 3 of type dbl
	fit	lwr	upr
1	355.5126	337.1189	373.9063

A matrix: 1 × 3 of type dbl
	fit	lwr	upr
1	355.5126	337.1189	373.9063

Tests of quadratic effect are the same

galileo0.lm = lm(Distance ~ Height, data=galileo)
anova(galileo0.lm, galileo1.lm)
anova(galileo0.lm, galileo2.lm)

A anova: 2 × 6
	Res.Df	RSS	Df	Sum of Sq	F	Pr(>F)
	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
1	5	5671.2063	NA	NA	NA	NA
2	4	744.0781	1	4927.128	26.48716	0.006760485

A anova: 2 × 6
	Res.Df	RSS	Df	Sum of Sq	F	Pr(>F)
	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
1	5	5671.2063	NA	NA	NA	NA
2	4	744.0781	1	4927.128	26.48716	0.006760485

Confidence intervals#

Suppose we want a $(1-\alpha)\cdot 100\%$ CI for $\sum_{j=0}^p a_j\beta_j$.
Just as in simple linear regression:

\[\sum_{j=0}^p a_j \widehat{\beta}_j \pm t_{1-\alpha/2, n-p-1} \cdot SE\left(\sum_{j=0}^p a_j\widehat{\beta}_j\right).\]

confint(bats.lm, level=0.90)
predict(bats.lm, list(Mass=300, Type="non-echolocating bats"), interval='confidence')

A matrix: 4 × 2 of type dbl
	5 %	95 %
(Intercept)	-3.2239868	6.06650127
Typenon-echolocating bats	-7.8142562	10.15127927
Typenon-echolocating birds	-1.5746672	10.77610686
Mass	0.0443021	0.07068873

A matrix: 1 × 3 of type dbl
	fit	lwr	upr
1	19.83839	13.40731	26.26948

$T$-statistics revisited#

Of course, these confidence intervals are based on the standard ingredients of a $T$-statistic.

Suppose we want to test

(13)#\[\begin{equation} H_0:\sum_{j=0}^p a_j\beta_j= h. \end{equation}\]

As in simple linear regression, it is based on

(14)#\[\begin{equation} T = \frac{\sum_{j=0}^p a_j \widehat{\beta}_j - h}{SE(\sum_{j=0}^p a_j \widehat{\beta}_j)}. \end{equation}\]

If $H_0$ is true, then $T \sim t_{n-p-1}$, so we reject $H_0$ at level $\alpha$ if

(15)#\[\begin{equation} \begin{aligned} |T| &\geq t_{1-\alpha/2,n-p-1}, \qquad \text{ OR} \\ p-\text{value} &= {\tt 2*(1-pt(|T|, n-p-1))} \leq \alpha. \end{aligned} \end{equation}\]

Let’s do a quick calculation to remind ourselves the relationships of the variables in the table above.

T_Mass = 0.057495 / 0.007557
P_Mass = 2 * (1 - pt(abs(T_Mass), 16))
c(T_Mass, P_Mass)

7.60817784835252
1.05724836840793e-06

summary(bats.lm)$coef

A matrix: 4 × 4 of type dbl
	Estimate	Std. Error	t value	Pr(>\|t\|)
(Intercept)	1.42125723	2.660683583	0.534170	6.005680e-01
Typenon-echolocating bats	1.16851155	5.145112379	0.227111	8.232139e-01
Typenon-echolocating birds	4.60071984	3.537112527	1.300699	2.117840e-01
Mass	0.05749542	0.007556812	7.608422	1.056817e-06

One-sided tests#

Suppose, instead, we wanted to test the one-sided hypothesis

(16)#\[\begin{equation} H_0:\sum_{j=0}^p a_j\beta_j \leq h, \ \text{vs.} \ H_a: \sum_{j=0}^p a_j\beta_j > h \end{equation}\]

If $H_0$ is true, then $T$ is no longer exactly $t_{n-p-1}$ but we still have

(17)#\[\begin{equation} \mathbb{P}\left(T > t_{1-\alpha, n-p-1}\right) \leq 1 - \alpha \end{equation}\]

We reject $H_0$ at level $\alpha$ if

(18)#\[\begin{equation} \begin{aligned} T &\geq t_{1-\alpha,n-p-1}, \qquad \text{ OR} \\ p-\text{value} &= {\tt (1-pt(T, n-p-1))} \leq \alpha. \end{aligned} \end{equation}\]

Standard error of $\sum_{j=0}^p a_j \widehat{\beta}_j$#

In order to form these $T$ statistics, we need the $SE$ of our estimate $\sum_{j=0}^p a_j \widehat{\beta}_j$.
Based on matrix approach to regression

(19)#\[\begin{equation} SE\left(\sum_{j=0}^p a_j\widehat{\beta}_j \right) = SE\left(a^T\widehat{\beta} \right) = \sqrt{\widehat{\sigma}^2 \cdot a^T (X^TX)^{-1} a}. \end{equation}\]

Don’t worry too much about specific implementation – for much of the effects we want R will do this for you in general.

X = model.matrix(bats.lm)
sigma.hat = sqrt(sum(resid(bats.lm)^2 / 16))
cov.beta = sigma.hat^2 * solve(t(X) %*% X)
cov.beta

A matrix: 4 × 4 of type dbl
	(Intercept)	Typenon-echolocating bats	Typenon-echolocating birds	Mass
(Intercept)	7.079237129	-6.26372902	-6.64565865	-1.647491e-03
Typenon-echolocating bats	-6.263729023	26.47218139	13.26936531	-2.661969e-02
Typenon-echolocating birds	-6.645658653	13.26936531	12.51116503	-1.338123e-02
Mass	-0.001647491	-0.02661969	-0.01338123	5.710541e-05

vcov(bats.lm)

A matrix: 4 × 4 of type dbl
	(Intercept)	Typenon-echolocating bats	Typenon-echolocating birds	Mass
(Intercept)	7.079237129	-6.26372902	-6.64565865	-1.647491e-03
Typenon-echolocating bats	-6.263729023	26.47218139	13.26936531	-2.661969e-02
Typenon-echolocating birds	-6.645658653	13.26936531	12.51116503	-1.338123e-02
Mass	-0.001647491	-0.02661969	-0.01338123	5.710541e-05

The standard errors of each coefficient estimate are the square root of the diagonal entries. They appear as the Std. Error column in the coef table.

sqrt(diag(vcov(bats.lm)))
summary(bats.lm)$coef[,2]

(Intercept): 2.66068358303546
Typenon-echolocating bats: 5.14511237921139
Typenon-echolocating birds: 3.53711252678651
Mass: 0.00755681226189849

(Intercept): 2.66068358303546
Typenon-echolocating bats: 5.14511237921139
Typenon-echolocating birds: 3.53711252678651
Mass: 0.00755681226189849

Prediction / forecasting interval#

Basically identical to simple linear regression.
Prediction interval at $X_{1,new}, \dots, X_{p,new}$:

(20)#\[\begin{equation} \begin{aligned} \widehat{\beta}_0 + \sum_{j=1}^p X_{j,new} \widehat{\beta}_j\pm t_{1-\alpha/2, n-p-1} \times & \\ \qquad \sqrt{\widehat{\sigma}^2 + SE\left(\widehat{\beta}_0 + \sum_{j=1}^p X_{j,new}\widehat{\beta}_j\right)^2} & \end{aligned} \end{equation}\]

Questions about many (combinations) of $\beta_j$’s#

In multiple regression we can ask more complicated questions than in simple regression.
For instance, in bats.lm we could ask whether Type is important at all?
These questions can be answered answered by $F$-statistics.

Dropping one or more variables#

Suppose we wanted to test the above hypothesis Formally, the null hypothesis is:

\[ H_0: \beta_1=\beta_2=0 \]

The alternative is

\[ H_a = \text{one of $ \beta_1,\beta_2$ is not 0}. \]

This test is an $F$-test based on two models

(21)#\[\begin{equation} \begin{aligned} \text{Full:} & \qquad \texttt{Energy $\widetilde{}$ Type + Mass} \\ \text{Reduced:} & \qquad \texttt{Energy $\widetilde{}$ Mass} \\ \end{aligned} \end{equation}\]

$SSE$ of a model#

In the graphic, a “model”, ${\cal M}$ is a subspace of $\mathbb{R}^n$ (e.g. column space of ${X}$).
Least squares fit = projection onto the subspace of ${\cal M}$, yielding predicted values $\widehat{Y}_{{\cal M}}$
Error sum of squares:

\[SSE({\cal M}) = \|Y - \widehat{Y}_{{\cal M}}\|^2.\]

Least squares for $F$ statistic#

{height=400 fig-align=”center”}

Fits of a full and reduced model $\hat{Y}_F$ and $\hat{Y}_R$
The difference $\hat{Y}_F-\hat{Y}_R$.

Right triangle for $F$ statistic#

{height=300 fig-align=”center”}

Sides of the triangle: $SSE_R-SSE_F$, $SSE_F$
Hypotenuse: $SSE_R$

Right triangle with full and reduced model: degrees of freedom#

{height=300 fig-align=”center”}

Sides of the triangle: $df_R-df_F$, $df_F$
Hypotenuse: $df_R$

$F$-statistic for $H_0:\beta_{1}=\beta_{2}=0$#

We compute the $F$ statistic the same to compare any two (nested) models

(22)#\[\begin{equation} \begin{aligned} F &=\frac{\frac{SSE(R) - SSE(F)}{2}}{\frac{SSE(F)}{n-1-p}} \\ & \sim F_{2, 16} \qquad (\text{if $H_0$ is true}) \end{aligned} \end{equation}\]

Reject $H_0$ at level $\alpha$ if $F > F_{1-\alpha, 2, 16}$.

reduced.lm = lm(Energy ~ Mass, data=bats)
anova(reduced.lm, bats.lm)

A anova: 2 × 6
	Res.Df	RSS	Df	Sum of Sq	F	Pr(>F)
	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
1	18	528.8563	NA	NA	NA	NA
2	16	450.0292	2	78.82704	1.401278	0.2749315

General $F$-tests#

Given two models $R \subset F$ (i.e. $R$ is a subspace of $F$), we can consider testing

(23)#\[\begin{equation} H_0: \text{$R$ is adequate (i.e. $\mathbb{E}(Y) \in R$)} \end{equation}\]

(24)#\[\begin{equation} H_a: \text{$F$ is adequate (i.e. $\mathbb{E}(Y) \in F$)} \end{equation}\]

The least squares picture has models $X_R$ and $X_F=X_R+(X_F \perp X_R) \dots$

The test statistic is

(25)#\[\begin{equation} F = \frac{(SSE(R) - SSE(F)) / (df_R - df_F)}{SSE(F)/df_F} \end{equation}\]

If $H_0$ is true, $F \sim F_{df_R-df_F, df_F}$ so we reject $H_0$ at level $\alpha$ if $F > F_{1-\alpha, df_R-df_F, df_F}$.

Constraining coefficients#

Suppose we wanted to test $H_0$: the line for non-echolocating bats has the same intercept as the line for non-echolocating birds.
Can be expressed as $H_0:\beta_1=\beta_2$ in bats.lm.

Strategy 1: fit a model in which this is forced to be true#

null_group = rep(1, nrow(bats))
null_group[bats$Type=="echolocating bats"] = 2
bats$null_group = factor(null_group)
null_bats.lm = lm(Energy ~ Mass + null_group, data=bats)
anova(null_bats.lm, bats.lm)

A anova: 2 × 6
	Res.Df	RSS	Df	Sum of Sq	F	Pr(>F)
	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
1	17	476.6541	NA	NA	NA	NA
2	16	450.0292	1	26.62481	0.9465984	0.345067

Strategy 2: a $T$-statistic#

Hypothesis is $H_0:\beta_1-\beta_2=0$
This method doesn’t require fitting the special model null_bats.lm!
Can be generalized to $F$ tests (hypotheses involving multiple contrasts of $\beta$)

A = c(0,1,-1,0)
var_diff = sum(A * vcov(bats.lm) %*% A)
se_diff = sqrt(var_diff)
T = sum(coef(bats.lm) * A) / se_diff
T^2

0.946598424772437

Math aside: general linear hypothesis#

Suppose we want to test the null hypothesis

(26)#\[\begin{equation} H_0:C_{q \times (p+1)}\beta_{(p+1) \times 1} = h \end{equation}\]

Alternative is

(27)#\[\begin{equation} H_a :C_{q \times (p+1)}\beta_{(p+1) \times 1} \neq h. \end{equation}\]

Math aside: $F$ statistic in general linear hypothesis#

Numerator

\[ (C\hat{\beta}-h)^T \left(C(X^TX)^{-1}C^T \right)^{-1} (C\hat{\beta}-h) / q \]

Denominator: the usual MSE
We just used special case $q=1$ above…

Multiple Linear Regression Inference

Contents

Multiple Linear Regression Inference#

Download#

Outline#

Energy costs of echolocation#

Fitting a model#

Other models#

Case study B: Galileo’s data#

Confidence intervals#

\(T\)-statistics revisited#

One-sided tests#

Standard error of \(\sum_{j=0}^p a_j \widehat{\beta}_j\)#

Prediction / forecasting interval#

Questions about many (combinations) of \(\beta_j\)’s#

Dropping one or more variables#

\(SSE\) of a model#

Least squares for \(F\) statistic#

Right triangle for \(F\) statistic#

Right triangle with full and reduced model: degrees of freedom#

\(F\)-statistic for \(H_0:\beta_{1}=\beta_{2}=0\)#

General \(F\)-tests#

Constraining coefficients#

Strategy 1: fit a model in which this is forced to be true#

Strategy 2: a \(T\)-statistic#

Math aside: general linear hypothesis#

Math aside: \(F\) statistic in general linear hypothesis#