Ctrl+K

Alternatives to T

Alternatives to T#

Download#

Outline#

  • Case studies:

    1. Shuttle O-ring incidents

    2. Cognitive load in math problems

  • Robustness and resistance of two-sample \(t\)-tests

  • Transformations

require(ggplot2)
set.seed(0)

Loading required package: ggplot2

Case study A: O-rings failing to seal fuel#

  • Is there a difference between Cool(<65F) and Warm (>65F)?

  • Temperature on launch day: 29F.

orings = read.csv('https://raw.githubusercontent.com/StanfordStatistics/stats191-data/main/Sleuth3/orings.csv', header=TRUE)
orings$Incidents[orings$Launch == 'Cool']
orings$Incidents[orings$Launch == 'Warm']
  1. 1
  2. 1
  3. 1
  4. 3
  1. 0
  2. 0
  3. 0
  4. 0
  5. 0
  6. 0
  7. 0
  8. 0
  9. 0
  10. 0
  11. 0
  12. 0
  13. 0
  14. 0
  15. 0
  16. 0
  17. 0
  18. 1
  19. 1
  20. 2

What test to use?#

  • Samples are really small

  • No sense in which they could be normally distributed…

Permutation test#

  • Decide a test statistic \(T\) comparing Cool(<65F) to Warm (>65F). Could be the two-sample \(t\) test statistic

  • Under \(H_0:\) Cool(<65F) has the same distribution Warm (>65F) suppose we:

    1. Shuffle the response in the two samples by a random ordering \(\sigma\) (called a permutation)

    2. Recompute the statistic yielding \(T(\sigma)\)

Permutation test in practice#

Build up a reference distribution under \(H_0\)#

B = 10000 # n_permutations
null_stats = rep(NA, B)
N = nrow(orings)
for (i in 1:B) {
    idx = sample(N, N, replace=FALSE)
    orings_star = data.frame(Incidents=orings$Incidents[idx],
                             Launch=orings$Launch)
    null_stats[i] = t.test(Incidents ~ Launch, data=orings_star)$stat
}

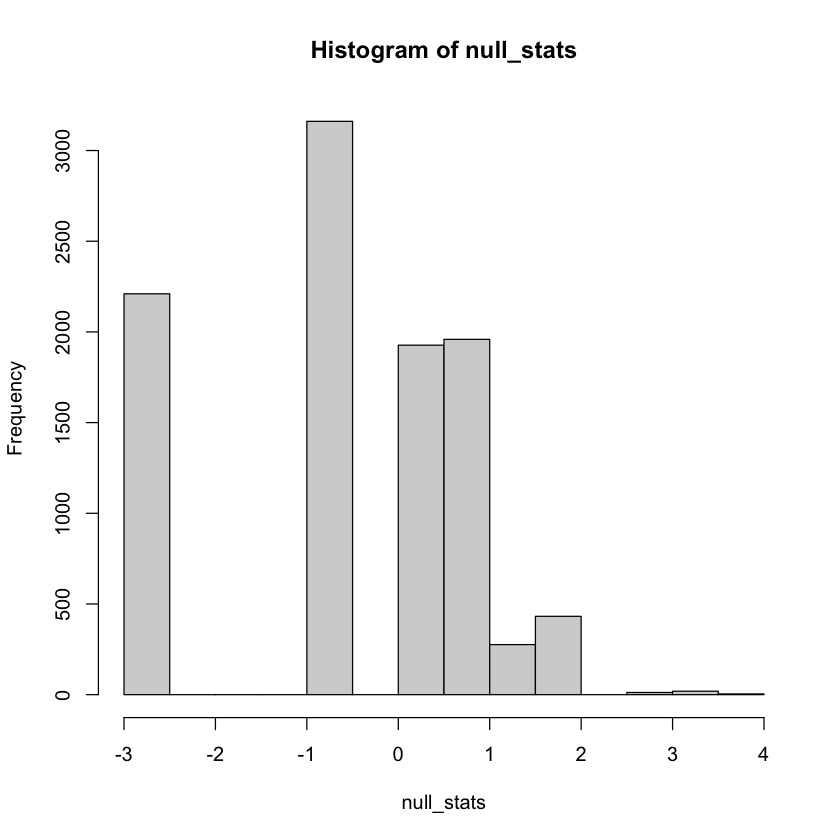
Histogram of \(t\)-statistic under \(H_0\)#

  • Doesn’t look \(t\)-shaped at all… but test is valid. Why?

  • Under \(H_0\): shuffling the response doesn’t change the distribution!

hist(null_stats)
../../_images/a0987d4ce16cde8cfd43a1294edd4438a7ad05ea867c066ed82a19ca437964e4.png

Compute a \(p\)-value#

observed = t.test(Incidents ~ Launch, data=orings)$stat
observed
mean(null_stats > observed)
t: 2.53163615804613
0.0023

Rank Sum Test#

  • One can use any test statistic for permutation test…

  • Only tests null \(H_0\): distributions are the same.

  • What should we use for \(H_a\)?

Case study B: difference in cognitive load#

  • Time to solve math problems under two different presentations

  • Small sample size, not normal?

cognitive_load = read.csv('https://raw.githubusercontent.com/StanfordStatistics/stats191-data/main/Sleuth3/cognitive_load.csv', header=TRUE)
cognitive_load
A data.frame: 28 × 3
TimeTreatmentCensored
<int><chr><int>
68Modified 0
70Modified 0
73Modified 0
75Modified 0
77Modified 0
80Modified 0
80Modified 0
132Modified 0
148Modified 0
155Modified 0
183Modified 0
197Modified 0
206Modified 0
210Modified 0
130Conventional0
139Conventional0
146Conventional0
150Conventional0
161Conventional0
177Conventional0
228Conventional0
242Conventional0
265Conventional0
300Conventional1
300Conventional1
300Conventional1
300Conventional1
300Conventional1

Rank sum test#

  • Rank the outcome

  • \(T\) = Sum the ranks in one of the groups (14 of 28 are Modified)

  • Under \(H_0:\) distributions are identical, \(T\) has distribution the sum of 14 ranks in a random permutation…

cognitive_load$R = rank(cognitive_load$Time)
rank_sum = with(cognitive_load, sum(R[Treatment == 'Modified']))
rank_sum
W = 14^2 + 14*15/2 - rank_sum
c(W, 14*14-W)
137
  1. 164
  2. 32

Rank sum test#

  • Using a builtin test

wilcox.test(Time ~ Treatment,
            data=cognitive_load,
            alternative='greater')

Warning message in wilcox.test.default(x = DATA[[1L]], y = DATA[[2L]], ...):
“cannot compute exact p-value with ties”

	Wilcoxon rank sum test with continuity correction

data:  Time by Treatment
W = 164, p-value = 0.001271
alternative hypothesis: true location shift is greater than 0

Rank sum test#

Null distribution (ignoring ties)#

null_sample = runif(28)
null_treat = c(rep('M', 14), rep('U', 14))
null_df = data.frame(S=null_sample, T=null_treat)
null_df$R = rank(null_df$S)
with(null_df, sum(R[T=='M']))
202

  • R uses a distributional approximation…

Confidence interval#

wilcox.test(Time ~ Treatment,
            data=cognitive_load,
            alternative='two.sided',
            conf.int=TRUE)

Warning message in wilcox.test.default(x = DATA[[1L]], y = DATA[[2L]], ...):
“cannot compute exact p-value with ties”

Warning message in wilcox.test.default(x = DATA[[1L]], y = DATA[[2L]], ...):
“cannot compute exact confidence intervals with ties”

	Wilcoxon rank sum test with continuity correction

data:  Time by Treatment
W = 164, p-value = 0.002542
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
  57.00007 159.99998
sample estimates:
difference in location 
                    94

  • What parameter is this estimating?

Shift alternative#

{height=400 fig-align=”center”}

  • \(H_a:\) the difference between groups is a simple shift

  • Other interpretations: estimating median of difference…

Paired data#

  • There are plenty of other non-parametric tests out there

Signed rank test for paired data (i.e. schizophrenia)#

  • \(H_0:\) distributions are the same in each group..

  • \(\implies\) differences are symmetrically distributed around 0!

Symmetric null#

{height=400 fig-align=”center”}

  • \(H_0:\) distribution is symmetric around 0.

Symmetric alternative#

{height=400 fig-align=”center”}

  • \(H_a:\) distribution is symmetric around \(\delta\).

Example of signed rank schizophrenia#

schizophrenia = read.csv('https://raw.githubusercontent.com/StanfordStatistics/stats191-data/main/Sleuth3/schizophrenia.csv', header=TRUE)
with(schizophrenia, wilcox.test(Affected, Unaffected), paired=TRUE)

Warning message in wilcox.test.default(Affected, Unaffected):
“cannot compute exact p-value with ties”

	Wilcoxon rank sum test with continuity correction

data:  Affected and Unaffected
W = 71.5, p-value = 0.09295
alternative hypothesis: true location shift is not equal to 0

Compare to t.test#

with(schizophrenia, t.test(Affected - Unaffected))

	One Sample t-test

data:  Affected - Unaffected
t = -3.2289, df = 14, p-value = 0.006062
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.3306292 -0.0667041
sample estimates:
 mean of x 
-0.1986667
Contents